Peatükk 3 Andmestike rühmitamine
Pideva tunnuse rühmitamine tähendab andmete jaotamist gruppidesse või kategooriatesse vastavalt nende väärtustele. See on oluline statistilise analüüsi meetod, kui soovime analüüsida suurt hulka andmeid ning leida seoseid või mustreid nende vahel.
Pideva tunnuse rühmitamine võib olla vajalik mitmel põhjusel:
Andmete lihtsustamine. Pidevate tunnuste rühmitamine võib muuta andmed hõlpsamini tõlgendatavaks ja analüüsitavaks, eriti juhul, kui on suur hulk erinevaid väärtusi.
Seoste või trendide avastamine. Rühmitades pidevaid tunnuseid, võime avastada seoseid või mustreid erinevate gruppide vahel. See võib aidata mõista näiteks, kuidas üks muutuja mõjutab teist või millised tegurid on omavahel seotud.
Statistilise analüüsi täpsus. Pidevate tunnuste rühmitamine võib parandada statistiliste analüüside täpsust ja usaldusväärsust, kuna see võib aidata vähendada andmete varieeruvust ning korrigeerida võimalikke moonutusi.
Seega on pideva tunnuse rühmitamine oluline statistilise analüüsi tööriist, mis aitab andmeid paremini mõista ja interpreteerida ning seeläbi teha järeldusi ja otsuseid põhinevalt faktidel ja statistilistel seostel.
3.1 Jaotused
3.1.1 Empiiriline jaotus
Empiiriline jaotus on statistilise andmestiku jaotus, mis põhineb tegelikel vaatlustel või mõõtmistel. See erineb teoreetilisest jaotusest, mis on abstraktne ja ideaalne jaotus, mida kasutatakse statistilistes mudelites ja analüüsides.
Empiiriline jaotus saadakse andmete kogumisel ja nende analüüsimisel, et mõista nähtuse tegelikku jaotust ja omadusi. See võib olla esitatud graafikuna (nt histogrammina) või matemaatilise mudelina, mis kirjeldab andmestiku jaotust.
Empiirilise jaotuse kasutamine on oluline, et saada parem arusaam uuritavast populatsioonist või nähtusest ning teha usaldusväärseid järeldusi statistiliste analüüside põhjal.
3.1.2 Teoreetiline jaotus
Teoreetiline jaotus on statistikas abstraktne kontseptsioon, mis kirjeldab tõenäosust, et mingi nähtuse väärtus võtab teatud vahemiku või konkreetse väärtuse. Teoreetiline jaotus arvutatakse tavaliselt matemaatiliste mudelite abil ning see aitab meil mõista andmete tõenäosuslikku käitumist mingi statistilise populatsiooni või nähtuse puhul. Teoreetilised jaotused on olulised statistiliste analüüside läbiviimisel ning nende põhjal saab teha järeldusi ja prognoose erinevate metsandustega seotud uuringute kohta.
3.2 Histogramm
Histogramm ehk sagedusjaotuse tulpdiagramm on graafiline esitusviis andmehulga sageduste jaotumise näitamiseks. Histogramm koosneb üksteise kõrvale paigutatud tulpadest, kus iga tulp esindab teatud vahemikku või klassi, ning selle kõrgus näitab antud klassi sagedust. Horisontaaltelg esitab klasside vahemikke või kategooriaid ning vertikaaltelg näitab vastavate klasside sagedusi või sageduste suhtarvu. Histogrammi abil saab hinnata andmehulga jaotust ning tuvastada erinevaid tendentse ja mustreid andmetes. Histogrammi loomise eesmärgiks on anda visuaalne ülevaade andmete koondumisest ja levikust ning seeläbi paremini mõista andmete struktuuri. Histogrammi loomisel on oluline valida sobiv klassilaius, mis võimaldab õigesti tõlgendada ja analüüsida andmeid. Histogramm on oluline tööriist statistilise info esitamiseks ja mõistmiseks nii akadeemilistes kui ka praktilistes seadetes, sealhulgas metsanduses.
Olgu juhuslikuks suuruseks puu diameeter. Antud näites on esitatud Järvseljal kvartalis 252 kasvanud 75 aasta vanuse naadisaariku saarepuude diameetri empiiriline jaotus proovitüki kluppimisandmete järgi.
3.2.1 R keskkonnas histogrammi loomine
Esmalt loome pidevast tunnusest mõned juhuslikud andmed ning seejärel kuvame nende andmete põhjal histogrammi.
Histogramm
# Laadime proovitükkide andmed
df <- readxl::read_excel("data/naited.xlsx","prt_andmed")
# koostame diameetrite histogrammi
ggplot(df, aes(d)) +
geom_histogram(
aes(y = after_stat(density)),
bins = 15,
fill = "white",
color = "black"
) +
geom_density(color = "red", lwd = 1) +
labs(y = "f(x)")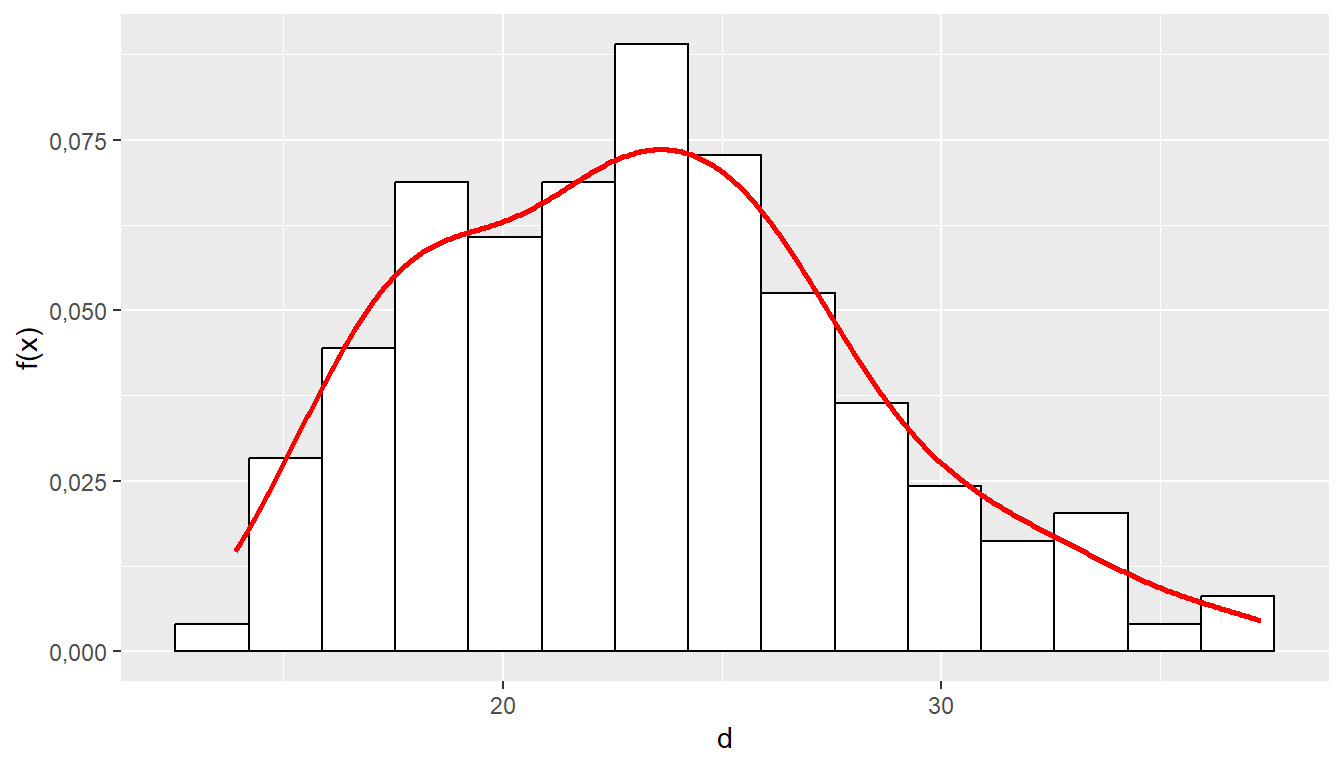
Joonis 3.1. Histogramm
See kood loob R-keeles ggplot2 paketiga graafiku, mis visualiseerib andmete jaotust. Vaatame seda samm-sammult:
ggplot(df, aes(x)): See alustab graafiku loomist.dfon andmetabel, mis sisaldab andmeid.aes(x)määrab, et x-teljele kuvatakse muutujatx. See on graafiku “põhi”, millele järgnevad kihid lisatakse.geom_histogram(...): See lisab histogrammi.geom_histogram()funktsioon loob histogrammi, mis näitab andmete sagedust erinevatesse gruppidesse jaotatuna.aes(y=after_stat(density))on oluline osa. See määrab, et y-teljel kuvatakse tihedust (density), mitte lihtsalt sagedust (count).after_stat()funktsiooniga pääsetakse ligi statistilisele väärtusele, mis arvutatakse histogrammi joonistamisel. Tihedus on normaliseeritud sagedus, nii et histogrammi pindala on 1. See võimaldab histogrammi ja tihedusfunktsiooni kõrvuti kuvada.fill="white"määrab histogrammi kastide sisemise värvi valgeks.color="black"määrab histogrammi kastide piirjoone värvi mustaks.
geom_density(color="red", lwd=1): See lisab tihedusfunktsiooni graafikule.geom_density()funktsioon arvutab ja joonistab andmete tihedusfunktsiooni, mis on silutud kõver, mis näitab andmete jaotuse kuju.color="red"määrab tihedusfunktsiooni joone värvi punaseks.lwd=1määrab joone paksuse (line width) 1-ks.
labs(y = "f(x)"): See lisab y-teljele sildi “f(x)”. See on hea tava, et telgi selgelt märgistada, eriti kui y-telg näitab tihedust, mitte sagedust. “f(x)” on levinud tähistus tõenäosustihedusfunktsioonile (probability density function).
Sageduste arvutamine
Tulpdiagrammile võib eelnevalt välja arvutada antud sagedused. Selleks saab kasutada funktsiooni cut(), mis vajab rühmade piire sisendiks ning seejärel saab juba funktsiooniga table() loendada kokku iga rühma liikmete arvu.
3.2.2 Exceli keskkonnas histogrammi loomine
3.2.2.1 Histogramm
Histogrammi loomiseks Excelis peab andmed esmalt sisestama tabelisse ja seejärel kasutama selle jaoks sobivat tööriista.
- Sisesta pideva tunnuse väärtused Exceli tabelisse.
- Vali need lahtrid, kuhu soovid luua histogrammi.
- Mine menüüsse “Lisa” ja vali “Diagramm”.
- Vali “Histogramm” ja klikka “OK”.
- Seejärel on võimalik vormindada telje suvandeid, millega määratakse rühmade (MS Exceli keskkonnas nimetusega “salv”) parameetrid.
3.2.2.2 Sageduste arvutamine
MS Exceli funktsioon FREQUENCY() võimaldab kasutajatel määrata, kui sageli väärtused esinevad teatud väärtusvahemikes. See funktsioon sobib hästi suurte andmekogumite analüüsimiseks, et mõista andmete jaotust ilma iga üksiku väärtuse manuaalse üle vaatamiseta.
Enne FREQUENCY() funktsiooni kasutamist peate määrama rühmade vahemike piirid, millesse soovite oma andmed jaotada. Need piirid tuleks sisestada eraldi veergu Exceli töölehel. Näiteks, kui soovite analüüsida testitulemusi vahemikus 0-100, võite määrata piirid 0, 20, 40, 60, 80, 100.
- Andmete ja piiride sisestamine.
- Sisestage oma andmekogum ühte veergu (nt A2:A101).
- Sisestage vahemike piirid teise veergu (nt B2:B7, eeldades, et esitasite näiteks eelmises punktis toodud piirid).
- Funktsiooni rakendamine.
- Valige tühi ala, kuhu soovite tulemused väljastada. Sellel peaks olema sama palju lahtrid kui määratletud vahemike piire. Kui teil on 6 piiri, valige 6 lahtrit vertikaalselt.
- Sisestage
FREQUENCY()funktsioon. KunaFREQUENCY()on massiivifunktsioon, tuleb see sisestada massiivivalemiga. Algusesse minev andmevahemik on teie andmekogum ja teine vahemik on teie vahemike piirid. Näiteks:=FREQUENCY(A2:A101, B2:B7) - Pärast funktsiooni sisestamist lõpetage sisestus, vajutades Ctrl+Shift+Enter. Excel käitab nüüd
FREQUENCY()funktsiooni massiivina ja täidab valitud lahtrid andmete sagedustega, mis vastavad määratud vahemikele.