Peatükk 7 Mitme tunnuse koosanalüüs
Mitme tunnuse koosanalüüs hõlmab mitmesuguseid statistilisi meetodeid, mille abil uuritakse, kuidas erinevad tunnused omavahel seostuvad ja üksteist mõjutavad. See analüüs on oluline, kuna reaalsetes olukordades mõjutavad uuritavat tunnust sageli mitmed tegurid korraga. Koosanalüüsi eesmärk on selgitada välja seosed tunnuste vahel, mõista nende mõju uuritavale nähtusele ja teha prognoose. Tunnuste koosanalüüs aitab minimeerida riski, et olulised seosed jäävad kahe silma vahele.
7.1 Lineaarne regressioon
Lineaarne regressioon on statistiline meetod, mida kasutatakse lineaarse seose modelleerimiseks sõltuva muutuja (funktsioontunnuse) ja ühe või mitme sõltumatu muutuja (argumenttunnuse) vahel. Eesmärk on leida sirge (või hüpertasapind mitme muutuja puhul), mis kõige paremini kirjeldab andmepunktide hajumist. See “parim sobivus” tähendab, et leitud sirge minimeerib vertikaalsete vahemaade summat andmepunktide ja sirge vahel.
Lineaarse regressiooni peamine eesmärk on:
- Ennustamine. Prognoosida sõltuva muutuja väärtust uute, seni tundmatute sõltumatute muutujate väärtuste korral.
- Seose mõistmine. Mõista ja kvantifitseerida sõltumatute muutujate mõju sõltuvale muutujale. See aitab hinnata iga sõltumatu muutuja panust ja olulisust sõltuva muutuja varieerumises.
Lihtsa lineaarse regressiooni mudel (üks sõltumatu muutuja) on esitatav järgmise valemiga:
\[y_i = \beta_0 + \beta_1 x_i + \epsilon_i\]
kus:
- \(y_i\) on \(i\)-nda vaatluse sõltuv muutuja väärtus.
- \(x_i\) on \(i\)-nda vaatluse sõltumatu muutuja väärtus.
- \(\beta_0\) on regressioonisirge lõikepunkt (konstantne termin). See on \(y\) väärtus, kui \(x = 0\).
- \(\beta_1\) on regressioonisirge kalle (koefitsient). See näitab, kui palju sõltuv muutuja \(y\) muutub, kui sõltumatu muutuja \(x\) suureneb ühe ühiku võrra.
- \(\epsilon_i\) on veatermin, mis esindab kõiki muid faktoreid, mis mõjutavad \(y_i\), kuid mida mudelis ei arvestata. Eeldatakse, et veaterminid on juhuslikud, keskmise väärtusega null ja konstantse dispersiooniga.
Mitme lineaarse regressiooni mudel (mitu sõltumatut muutujat) on üldistus ülaltoodud mudelist:
\[y_i = \beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + ... + \beta_p x_{pi} + \epsilon_i\]
kus:
- \(x_{ji}\) on \(i\)-nda vaatluse \(j\)-nda sõltumatu muutuja väärtus (kus \(j=1, 2, ..., p\) ja \(p\) on sõltumatute muutujate arv).
- \(\beta_j\) on \(j\)-nda sõltumatu muutuja regressioonikoefitsient. See näitab, kui palju sõltuv muutuja \(y\) muutub, kui \(j\)-s sõltumatu muutuja \(x_j\) suureneb ühe ühiku võrra, eeldusel, et kõik teised sõltumatud muutujad jäävad konstantseks (ceteris paribus).
- \(\beta_0\) on lõikepunkt.
- \(\epsilon_i\) on veatermin.
Lineaarne regressioon arvutatakse tavaliselt vähimruutude meetodit (Ordinary Least Squares - OLS) kasutades. Vähimruutude meetodi eesmärk on minimeerida hälvete ruutude summat (RSS - Residual Sum of Squares) ehk ennustatud väärtuste ja tegelike väärtuste vahe ruutude summat.
RSS valem on:
\[RSS = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = \sum_{i=1}^{n} (y_i - (\beta_0 + \beta_1 x_{1i} + ... + \beta_p x_{pi}))^2\]
kus:
- \(n\) on vaatluste arv.
- \(\hat{y}_i = \beta_0 + \beta_1 x_{1i} + ... + \beta_p x_{pi}\) on mudeli poolt ennustatud \(y_i\) väärtus.
Vähimruutude meetodi kasutamiseks tuleb leida sellised \(\beta_0, \beta_1, ..., \beta_p\) väärtused, mis minimeerivad RSS. See saavutatakse osatuletiste võtmisega RSS-ist iga \(\beta_j\) suhtes ja nende tuletiste nulliga võrdumise seadmisega. See annab normaalvõrrandite süsteemi.
Maatriksvormis saab lineaarset regressioonimudelit ja vähimruutude lahendust esitada elegantselt. Olgu Y vektor sõltuvatest muutujatest, X disainmaatriks (mis sisaldab sõltumatuid muutujaid ja konstantsammast ühtedest lõikepunkti jaoks) ja \(\beta\) koefitsientide vektor. Mudel on:
\[\mathbf{Y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\epsilon}\]
kus:
- \(\mathbf{Y} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}\) on \(n \times 1\) vektor sõltuvate muutujate vaatlustest.
- \(\mathbf{X} = \begin{bmatrix} 1 & x_{11} & x_{21} & \cdots & x_{p1} \\ 1 & x_{12} & x_{22} & \cdots & x_{p2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{1n} & x_{2n} & \cdots & x_{pn} \end{bmatrix}\) on \(n \times (p+1)\) disainmaatriks. Esimene veerg on ühtedest lõikepunkti jaoks, ja järgmised veerud on sõltumatute muutujate vaatlused.
- \(\boldsymbol{\beta} = \begin{bmatrix} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_p \end{bmatrix}\) on \((p+1) \times 1\) vektor regressioonikoefitsientidest.
- \(\boldsymbol{\epsilon} = \begin{bmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n \end{bmatrix}\) on \(n \times 1\) vektor veaterminitest.
Vähimruutude lahendus koefitsientide vektorile \(\boldsymbol{\hat{\beta}}\) on antud järgmise valemiga:
\[\boldsymbol{\hat{\beta}} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y}\]
Eeldusel, et \((\mathbf{X}^T\mathbf{X})\) on pööratav. See on peamine valem regressioonikoefitsientide arvutamiseks.
Pärast regressioonimudeli arvutamist on oluline hinnata selle sobivust ja statistilist olulisust. Peamised teststatistikud ja hindamise meetodid on järgmised:
\(R^2\) ja kohandatud \(R^2\).
- \(R^2\) (determinatsioonikordaja). Mõõdab, kui suure osa sõltuva muutuja varieeruvusest suudab regressioonimudel seletada. \(R^2\) väärtused jäävad vahemikku 0 kuni 1. Mida lähemal on \(R^2\) väärtusele 1, seda paremini mudel andmeid sobitab.
- Valem \(R^2\) arvutamiseks: \[R^2 = 1 - \frac{RSS}{TSS} = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2}\] kus \(TSS\) on hälvete ruutude summa (Total Sum of Squares) ja \(\bar{y}\) on sõltuva muutuja keskmine väärtus.
- Kohandatud \(R^2\). Parandab \(R^2\) puudust, mis alati suureneb sõltumatute muutujate arvu lisandumisel, isegi kui need muutujad ei ole olulised. Kohandatud \(R^2\) karistab mudelit ebavajalike muutujate lisamise eest.
- Valem kohandatud \(R^2\) arvutamiseks: \[\text{Kohandatud } R^2 = 1 - \frac{(1-R^2)(n-1)}{n-p-1}\] kus \(n\) on vaatluste arv ja \(p\) on sõltumatute muutujate arv mudelis (ilma lõikepunktita).
RMSE (ruutkeskmine viga).
- RMSE mõõdab mudeli ennustusvigade standardhälvet. See annab aimu, kui suur on tüüpiline erinevus ennustatud ja tegelike väärtuste vahel. Madalam RMSE näitab paremat mudeli ennustustäpsust.
- Valem RMSE arvutamiseks: \[RMSE = \sqrt{\frac{RSS}{n}} = \sqrt{\frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{n}}\]
Koefitsientide statistiline olulisus (t-test).
- Iga regressioonikoefitsiendi \(\beta_j\) (välja arvatud \(\beta_0\)) puhul saab testida nullhüpoteesi \(H_0: \beta_j = 0\), mis tähendab, et \(j\)-ndal sõltumatul muutujal puudub seos sõltuva muutujaga (kui kõik teised muutujad on konstantsed).
- T-testi statistiku arvutamine koefitsiendi \(\beta_j\) jaoks: \[t = \frac{\hat{\beta}_j}{SE(\hat{\beta}_j)}\] kus \(SE(\hat{\beta}_j)\) on \(\hat{\beta}_j\) standardviga. Standardvea saab arvutada mudeli veaterminite dispersiooni ja disainmaatriksi \(\mathbf{X}\) põhjal.
- Saadud t-statistikut võrreldakse t-jaotuse kriitiliste väärtustega (või arvutatakse p-väärtus), et otsustada nullhüpoteesi tagasilükkamine. Madal p-väärtus (tavaliselt alla 0.05) viitab, et koefitsient on statistiliselt oluline ja sõltumatu muutuja avaldab olulist mõju sõltuvale muutujale.
Mudeli üldine olulisus (F-test).
- F-test testib nullhüpoteesi, et kõik regressioonikoefitsiendid (välja arvatud \(\beta_0\)) on samaaegselt null \(H_0: \beta_1 = \beta_2 = ... = \beta_p = 0\). See test hindab, kas mudel tervikuna on statistiliselt oluline ja kas on vähemalt üks sõltumatu muutuja, mis aitab sõltuva muutuja varieeruvust seletada.
- F-statistiku arvutamine: \[F = \frac{MSS}{MSE} = \frac{RSS_{null} - RSS_{mudel}}{RSS_{mudel}} \times \frac{n-p-1}{p}\] kus \(MSS\) on mudeli ruutude keskmine summa (Model Sum of Squares), \(MSE\) on vigade ruutude keskmine summa (Mean Squared Error), \(RSS_{null}\) on RSS mudeli korral, mis sisaldab ainult lõikepunkti (nullmudel), ja \(RSS_{mudel}\) on RSS uuritava mudeli korral.
- F-statistikut võrreldakse F-jaotuse kriitiliste väärtustega (või arvutatakse p-väärtus), et otsustada nullhüpoteesi tagasilükkamine. Madal p-väärtus (tavaliselt alla 0.05) viitab, et mudel on statistiliselt oluline.
7.2 Lineaarse regressiooni eelduste selgitus
Lineaarse regressiooni rakendamine on võimas meetod seoste modelleerimiseks, kuid selle tulemuste usaldusväärsus sõltub teatud eelduste täitmisest. Need eeldused tagavad, et vähimruutude meetod annab parimad võimalikud ja usaldusväärsed hinnangud regressioonikoefitsientidele ja mudeli statistilisele olulisusele. Vaatame neid eeldusi ükshaaval põhjalikumalt:
Lineaarsus. Eeldatakse, et sõltuva muutuja ja sõltumatute muutujate vaheline seos on lineaarne. See tähendab, et sõltuva muutuja muutuse ennustatakse iga sõltumatu muutuja ühiku muutuse kohta konstantse suurusega.
- Mida see tähendab. Graafiliselt kujutades peaks andmepunktide hajumine järgima sirget joont (lihtsa lineaarse regressiooni puhul) või hüpertasapinda (mitmese lineaarse regressiooni puhul). Formaalselt öeldes tähendab see, et oodatav väärtus sõltuvale muutujale on lineaarne funktsioon sõltumatutest muutujatest.
- Miks see oluline on. Kui tegelik seos ei ole lineaarne, siis lineaarse regressiooni mudel ei suuda seost adekvaatselt kirjeldada. Lineaarne mudel võib anda eksitavaid ennustusi ja valed järeldused muutujate seoste kohta.
- Kuidas kontrollida.
- Hajuvusdiagrammid. Sõltuva muutuja hajuvusdiagrammi joonistamine iga sõltumatu muutuja suhtes aitab visuaalselt hinnata lineaarsust.
- Jääkide diagrammid. Jääkide (tegelike ja ennustatud väärtuste vahe) diagrammi joonistamine ennustatud väärtuste või sõltumatute muutujate suhtes. Lineaarsuse korral peaks jääkide hajumine olema juhuslikult jaotunud nulljoone ümber, ilma süstemaatilise mustrita. Mitte-lineaarsuse korral võib diagrammil näha kõveraid mustreid.
- Mis juhtub, kui eeldus on rikutud. Lineaarne mudel võib anda halbu ennustusi ja valed järeldused.
- Mida teha.
- Muutujate transformeerimine. Sõltuva ja/või sõltumatute muutujate transformeerimine (näiteks logaritm, ruutjuur, ruut) võib mõnikord muuta mittelineaarse seose lineaarseks.
- Polünoomiline regressioon. Lineaarse mudeli asemel võib kasutada polünoomilist regressiooni, mis võimaldab modelleerida mittelineaarseid seoseid polünoomide abil.
- Mittelineaarne regressioon. Kui seos on teadaolevalt mittelineaarne ja transformatsioonid ei aita, võib kasutada mittelineaarset regressiooni meetodit, mis on spetsiifiliselt loodud mittelineaarsete seoste modelleerimiseks.
Sõltumatus. Iga vaatlus peab olema sõltumatu teistest vaatlustest. See tähendab, et ühe vaatluse väärtus ei tohiks olla mõjutatud teiste vaatluste väärtustest.
- Mida see tähendab. Iga andmepunkt peaks olema kogutud või genereeritud sõltumatult teistest andmepunktidest. Näiteks, kui me uurime individuaalsete inimeste andmeid, eeldame, et ühe inimese andmed ei mõjuta teise inimese andmeid.
- Miks see oluline on. Sõltumatuse eeldus on oluline standardvigade korrektseks hindamiseks ja seega ka statistilise olulisuse testide ja usaldusvahemike usaldusväärsuseks. Kui vaatlused on sõltuvad, siis standardvead võivad olla alahinnatud, mis viib valejäreldusteni statistilise olulisuse kohta (mudel näib statistiliselt olulisem kui see tegelikult on).
- Kuidas kontrollida.
- Andmete kogumise protsessi mõistmine. Hoolikalt tuleb kaaluda, kuidas andmed on kogutud. Kas on potentsiaalseid sõltuvuse allikaid? Näiteks aja-reas andmetes (andmed, mis on kogutud aja jooksul järjestikku) on sageli sõltuvus, kus eilne väärtus võib mõjutada tänast väärtust. Samuti võib sõltuvust esineda klasterandmetes (näiteks õpilased klassides, patsiendid arstides), kus grupis olevad vaatlused võivad olla sarnasemad kui grupidest väljaspool olevad vaatlused.
- Durbin-Watson test (aja-rea andmete korral). Durbin-Watson test on spetsiifiliselt loodud autokorrelatsiooni (sõltuvuse) tuvastamiseks jääkides aja-rea andmetes.
- Mis juhtub, kui eeldus on rikutud. Standardvead on ebatäpsed, mis teeb statistilised testid ja usaldusvahemikud ebausaldusväärseks.
- Mida teha.
- Aja-rea mudelid. Kui tegemist on aja-rea andmetega ja sõltuvus on autokorrelatsioon, võib kasutada aja-rea mudelite (näiteks ARIMA mudelid) asemel lineaarselt regressiooni.
- Segamõjudega mudelid (klasterandmete korral). Kui tegemist on klasterandmetega, võib kasutada segamõjudega mudeleid (mixed-effects models), mis võtavad arvesse grupisisese sõltuvuse.
- Robustsed standardvead. Teatud juhtudel, kui sõltuvust ei saa täielikult modelleerida, saab kasutada robustseid standardvigu (näiteks Huber-White standardvead), mis on vähem tundlikud sõltuvuse suhtes (kuigi need ei lahenda probleemi täielikult).
Homoskedastilisus. Jääkide dispersioon (variatsioon) peaks olema konstantne kõigi sõltumatute muutujate väärtuste korral. See tähendab, et jääkide “hajuvus” peaks olema ühtlane kogu regressioonisirge pikkuses. Heteroskedastilisus on homoskedastilisuse vastand ja tähendab, et jääkide dispersioon ei ole konstantne, vaid muutub sõltuvalt sõltumatute muutujate väärtustest.
- Mida see tähendab. Jääkide hajumisdiagrammil ennustatud väärtuste või sõltumatute muutujate suhtes peaks jääkide punktide “laius” olema enam-vähem sama kogu ulatuses.
- Miks see oluline on. Homoskedastilisus on oluline vähimruutude meetodi efektiivsuse tagamiseks. Kuigi vähimruutude meetod annab ikka erapooletud hinnangud koefitsientidele ka heteroskedastilisuse korral, on hinnangud ebaefektiivsed (neil on suurem dispersioon kui vaja oleks) ja standardvead on jälle ebatäpsed, mis mõjutab statistiliste testide ja usaldusvahemike usaldusväärsust.
- Kuidas kontrollida.
- Jääkide hajumisdiagrammid. Jääkide diagrammi joonistamine ennustatud väärtuste või iga sõltumatu muutuja suhtes. Homoskedastilisuse korral peaks jääkide hajumine olema juhuslik ja ühtlane riba ümber nulljoone. Heteroskedastilisuse korral võib diagrammil näha mustreid, näiteks jääkide “laiuse” suurenemine või vähenemine koos ennustatud väärtuste või sõltumatu muutuja väärtustega (näiteks “lehviku” kuju).
- Breusch-Pagan test ja White’i test. Need on formaalsed statistilised testid heteroskedastilisuse testimiseks. Need testid hindavad, kas jääkide ruudud on seotud sõltumatute muutujate või nende ruutudega.
- Mis juhtub, kui eeldus on rikutud. Vähimruutude hinnangud on ebaefektiivsed ja standardvead on ebatäpsed.
- Mida teha.
- Muutujate transformeerimine. Sõltuva muutuja transformeerimine (näiteks logaritm, ruutjuur) võib mõnikord vähendada heteroskedastilisust, eriti kui heteroskedastilisus on seotud sõltuva muutuja tasemega.
- Robustsed standardvead. Nagu sõltumatuse puhul, saab ka heteroskedastilisuse korral kasutada robustseid standardvigu (näiteks Huber-White standardvead). Need annavad usaldusväärsemad standardvead ja seega ka usaldusväärsemad statistilised testid ja usaldusvahemikud, isegi kui heteroskedastilisus on olemas.
- Kaalutud vähimruudud (Weighted Least Squares - WLS). WLS meetod on spetsiifiliselt loodud heteroskedastilisuse probleemi lahendamiseks. See meetod annab suuremad kaalud vaatlustele, millel on väiksem jääkide dispersioon, ja väiksemad kaalud vaatlustele, millel on suurem jääkide dispersioon, et “ühtlustada” variatsiooni.
Normaaljaotus. Jäägid peaksid olema ligikaudselt normaaljaotusega. See eeldus kehtib eelkõige statistiliste testide ja usaldusvahemike usaldusväärsuse jaoks, eriti väikeste valimite korral. Suurte valimite korral, tänu keskväärtusteoreemile, on regressioonikoefitsientide hinnangud ligikaudu normaalselt jaotunud isegi siis, kui jäägid ei ole täpselt normaalselt jaotunud (kuid siiski peaksid olema homoskedastilised ja sõltumatud).
- Mida see tähendab. Jääkide histogramm peaks meenutama kellakujulist normaaljaotust. Jääkide teoreetiline jaotus peaks olema normaalne.
- Miks see oluline on. Normaaljaotuse eeldus on oluline, et kasutada t-teste koefitsientide statistilise olulisuse testimiseks ja F-testi mudeli üldise olulisuse testimiseks, eriti väikeste valimite korral. Kui jäägid on normaalselt jaotunud, siis koefitsientide hinnangud on ka normaalselt jaotunud ja teststatistikud järgivad t- ja F-jaotusi vastavalt. Kui jäägid ei ole normaalselt jaotunud (eriti kui valim on väike), siis võivad testide p-väärtused ja usaldusvahemikud olla ebatäpsed.
- Kuidas kontrollida.
- Histogramm ja tihedusdiagramm. Jääkide histogrammi ja tihedusdiagrammi joonistamine aitab visuaalselt hinnata, kas jäägid on ligikaudu normaalselt jaotunud.
- Normaalsuse Q-Q diagramm (Quantile-Quantile plot). Q-Q diagramm võrdleb jääkide kvantiile teoreetilise normaaljaotuse kvantiilidega. Kui jäägid on normaalselt jaotunud, peaksid punktid Q-Q diagrammil paiknema ligikaudu sirgel joonel.
- Formaalsed normaalsuse testid. Näiteks Shapiro-Wilk test, Kolmogorov-Smirnov test, Jarque-Bera test. Need testid annavad statistilise p-väärtuse, mis hindab, kas jäägid erinevad oluliselt normaaljaotusest.
- Mis juhtub, kui eeldus on rikutud. Väikeste valimite korral võivad t-testid ja F-testid olla ebausaldusväärsed. Suurte valimite korral on lineaarsed regressioonitulemused sageli robustsed normaalsuse rikkumise suhtes (tänu keskväärtusteoreemile).
- Mida teha.
- Muutujate transformeerimine. Sõltuva muutuja transformeerimine võib mõnikord muuta jääkide jaotust normaalsemaks.
- Mitteparameetrilised meetodid. Kui normaalsuse rikkumine on tõsine ja valim on väike, võib kaaluda mitteparameetriliste regressioonimeetodite kasutamist, mis ei eelda normaaljaotust (kuid need meetodid võivad olla vähem võimsad kui lineaarne regressioon, kui eeldused on täidetud).
- Suur valim. Suurte valimite korral on lineaarne regressioon suhteliselt robustne normaalsuse rikkumise suhtes. Kui valim on piisavalt suur, ei pruugi normaalsuse eeldus olla nii kriitiline.
Multikollineaarsuse puudumine. Sõltumatud tunnused (argumenttunnused) ei tohiks omavahel tugevalt korreleeruda. Multikollineaarsus tekib siis, kui kaks või enam sõltumatut muutujat on omavahel tugevalt lineaarselt seotud.
- Mida see tähendab. See tähendab, et sõltumatud muutujad ei tohiks olla üksteise ennustajad. Näiteks, kui me modelleerime palku haridustaseme ja töökogemuse põhjal, võib multikollineaarsus tekkida, kui haridustase ja töökogemus on tugevalt korreleeritud (kõrgema haridusega inimestel on tavaliselt rohkem töökogemust).
- Miks see oluline on. Multikollineaarsus ei mõjuta mudeli ennustusvõimet tervikuna, kuid see teeb üksikute sõltumatute muutujate mõju eristamise raskeks ja ebastabiilseks. Regressioonikoefitsiendid muutuvad ebatäpseks (suured standardvead) ja ebastabiilseks (väikesed muutused andmetes võivad põhjustada suuri muutusi koefitsientides). Samuti võib see muuta koefitsientide märke ootamatuks.
- Kuidas kontrollida.
- Korrelatsioonimaatriks. Sõltumatute muutujate vahelise korrelatsioonimaatriksi arvutamine ja korrelatsioonikordajate (eriti Pearsoni korrelatsioonikordajate) vaatamine. Kõrged korrelatsioonikordajad (näiteks absoluutväärtus üle 0.7 või 0.8) võivad viidata multikollineaarsusele.
- VIF (Variance Inflation Factor - dispersiooni paisutustegur). VIF arvutatakse iga sõltumatu muutuja jaoks. See mõõdab, kui palju iga muutuja standardviga on paisunud multikollineaarsuse tõttu. Kõrged VIF väärtused (tavaliselt üle 5 või 10) viitavad multikollineaarsusele.
- Mis juhtub, kui eeldus on rikutud. Regressioonikoefitsiendid on ebastabiilsed ja raskesti interpreteeritavad, standardvead paisuvad, mis teeb statistilised testid vähem võimsaks. Kuigi mudeli ennustusvõime tervikuna ei pruugi kannatada, on üksikute muutujate mõju raske hinnata.
- Mida teha.
- Muutujate eemaldamine. Kui multikollineaarsus on probleemiks, võib eemaldada mudelist ühe või mitu omavahel korreleeruvat muutujat. Tuleb valida, millised muutujad on teoreetiliselt või praktiliselt vähem olulised või redundantsed.
- Muutujate kombineerimine. Korreleeritud muutujad võib kombineerida üheks uueks muutujaks (näiteks summeerida või arvutada keskmist).
- PCA (Principal Component Analysis - peamiste komponentide analüüs) või PLS (Partial Least Squares - osalised vähimruudud) regressioon. Need meetodid on spetsiifiliselt loodud multikollineaarsuse probleemi lahendamiseks. PCA regressioon teisendab algsed muutujad uuteks, ortogonaalseteks (mitte-korreleeritud) komponentideks ja kasutab neid regressioonis. PLS regressioon on eriti kasulik, kui on palju sõltumatuid muutujaid ja multikollineaarsus on tugev.
- Regulariseerimine (näiteks Ridge regressioon või Lasso regressioon). Regulariseerimise meetodid aitavad vähendada multikollineaarsuse mõju, “kahandades” koefitsiente ja vähendades nende dispersiooni (kuigi nad võivad ka koefitsientide hinnanguid “biaseerida”).
7.3 Lineaarne regressioon R-is
Proovitükil on mõõdetud puudel diameetrid ja kõrgused. Eesmärgiks on leida lineaarse regressiooniga mudel, millega ennustada diameetrist puude kõrgust.
# Laadi alla 'readxl' pakett, et lugeda Exceli faili
library(readxl)
# Loe andmed Exceli failist ja konkreetselt töölehelt
andmed <- read_excel("data/naited.xlsx", sheet = "MA")
# Vaata, kuidas andmed välja näevad ja kontrolli veergude nimesid
head(andmed)# A tibble: 6 × 6
NR D H HV VP SHV
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 10 9.7 12.2 7.1 5.1 0.58
2 20 10.2 11.1 7.5 3.6 0.68
3 30 6.3 9.9 7 2.9 0.71
4 40 7.4 11 7.5 3.5 0.68
5 50 5.6 8.8 6.8 2 0.77
6 60 5.6 10.6 7.2 3.4 0.68# Lineaarse regressiooni mudeli loomine
# Valem H = f(D) tähendab, et H on sõltuv muutuja ja D on sõltumatu muutuja.
# R-is tähistatakse seda valemit kujul H ~ D
lm_1 <- lm(H ~ D, data = andmed)
# Mudeli kokkuvõtte kuvamine
summary(lm_1)
Call:
lm(formula = H ~ D, data = andmed)
Residuals:
Min 1Q Median 3Q Max
-2,1190 -0,6362 -0,0361 0,9079 1,9273
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5,6036 0,5427 10,32 1,0e-11
D 0,5481 0,0652 8,41 1,3e-09
Residual standard error: 1,15 on 32 degrees of freedom
Multiple R-squared: 0,688, Adjusted R-squared: 0,679
F-statistic: 70,7 on 1 and 32 DF, p-value: 1,32e-09library(ggplot2)
# Joonista punktgraafik koos regressioonisirgega
ggplot(andmed, aes(x = D, y = H)) +
geom_point() + # Lisa punktid andmete jaoks
geom_smooth(method = "lm", se = TRUE, color="red") +
xlim(0, 20) + ylim(0, 20)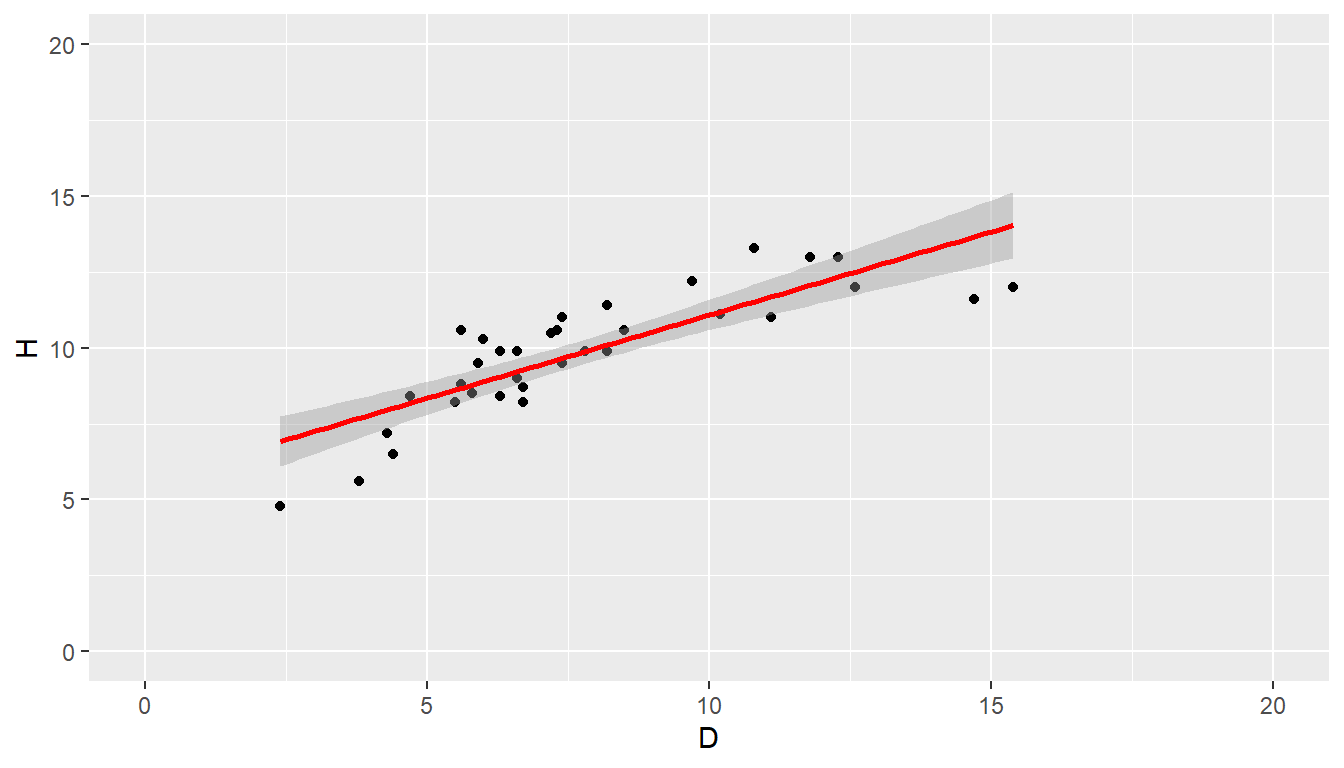
Joonis 7.1. Hajuvusdiagramm
Täiendame regressioonimudelit, kus argumenttunnuseks on naturaallogaritm diameetrist.
# Lineaarse regressiooni mudeli loomine
# R-is tähistatakse seda valemit kujul H ~ log(D)
summary(lm_2 <- lm(H ~ log(D), data = andmed))
Call:
lm(formula = H ~ log(D), data = andmed)
Residuals:
Min 1Q Median 3Q Max
-1,505 -0,532 -0,183 0,673 1,887
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0,871 0,799 1,09 0,28
log(D) 4,552 0,397 11,47 7,2e-13
Residual standard error: 0,909 on 32 degrees of freedom
Multiple R-squared: 0,804, Adjusted R-squared: 0,798
F-statistic: 131 on 1 and 32 DF, p-value: 7,2e-13Ning vaatame tulemust graafikul.
library(ggplot2)
# Joonista punktgraafik koos regressioonisirgega
ggplot(andmed, aes(x = D, y = H)) +
geom_point() + # Lisa punktid andmete jaoks
geom_smooth(method = "lm", formula = y~log(x), se = TRUE, color="red") +
xlim(0, 20) + ylim(0, 20)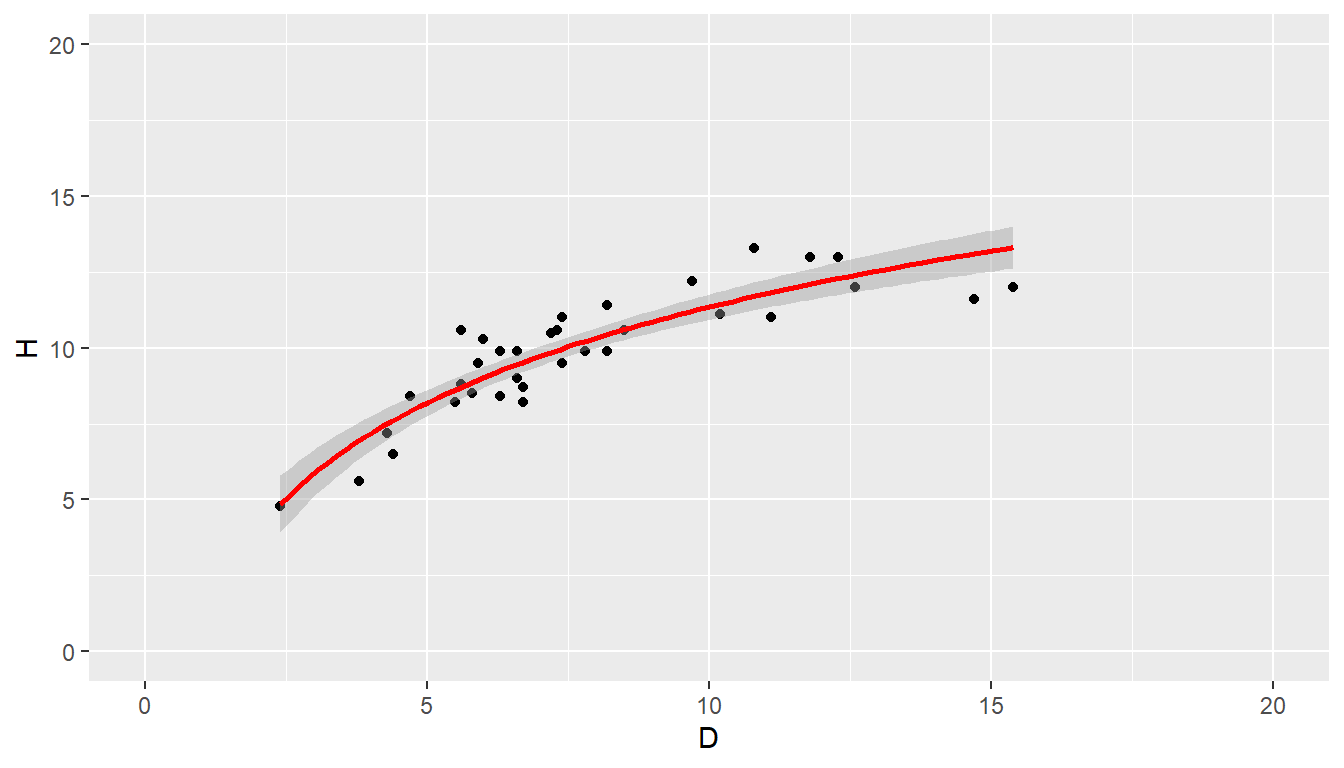
Joonis 7.2. Hajuvusdiagramm logaritmilise teisendusega
ANOVA (Analysis of Variance) on statistiline meetod, mida kasutatakse kahe või enama rühma keskmiste võrdlemiseks. Regressioonimudelite puhul saab ANOVA-t kasutada kahe mudeli võrdlemiseks, et näha, kas üks mudel selgitab oluliselt rohkem varieeruvust kui teine mudel.
Eeldused
Enne ANOVA kasutamist on oluline tagada, et andmed vastavad järgmistele eeldustele:
- Sõltuv tunnus peab olema pidev.
- Sõltumatud tunnused võivad olla nii pidevad kui ka kategoorilised.
- Vigade dispersioon peab olema konstantne (homoskedastsus).
- Vead peavad olema normaalselt jaotunud.
- Vaatlused peavad olema sõltumatud.
ANOVA läbiviimine
Antud juhul on meil kaks mudelit:
- Mudel 1.
H~D - Mudel 2.
H~log(D)
ANOVA abil saame võrrelda neid kahte mudelit, et näha, kas mudel 2 selgitab oluliselt rohkem varieeruvust kui mudel 1.
Analysis of Variance Table
Model 1: H ~ D
Model 2: H ~ log(D)
Res.Df RSS Df Sum of Sq F Pr(>F)
1 32 42,1
2 32 26,5 0 15,7 Tulemusest näeme, et esimese mudeli hälvete ruutude summa (RSS) on suurem (42,1308 > 26,46116), seega on teine mudel täpsem.
Hindame mudelite jääkide jaotust ning hindame, kas need vastavad normaaljaotusele.
par(mar=c(4,4,1,1), mgp=c(2, 0.7, 0))
plot(density(resid(lm_1), bw = 0.5), ylim=c(0, 0.4), main="", xlab="Jäägid", ylab="f(x)")
lines(density(resid(lm_2), bw = 0.5), col = 2)
abline(v = 0)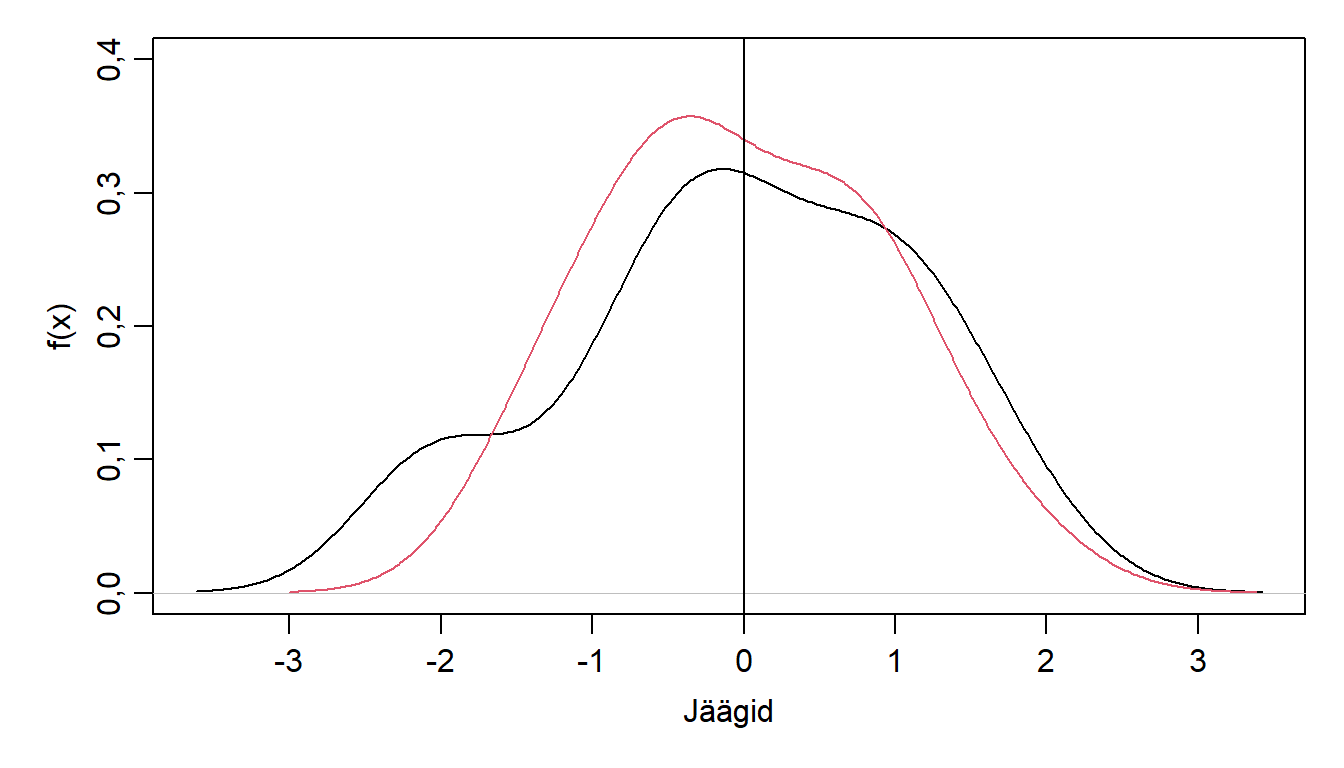
Joonis 7.3. Lineaarse regressiooni jääkide tihedusfunktsioon.
Shapiro-Wilk normality test
data: resid(lm_1)
W = 0,957, p-value = 0,2Sinu antud tulemus näitab järgmist:
- W = 0,95708. See on teststatistik. W väärtus, mis on lähedal 1-le, viitab sellele, et andmed on tõenäoliselt normaaljaotusega.
- p-value = 0,19958. See on olulisuse tõenäosus (p-väärtus). See näitab tõenäosust, et saaksid sarnase või ekstreemsema tulemuse, kui andmed tegelikult oleksid normaaljaotusega.
Järeldus
Kuna p-väärtus (0,95708) on suurem kui tavaline \(\alpha\)-tase 0,05, siis me ei saa nullhüpoteesi (et andmed on normaaljaotusega) ümber lükata. See tähendab, et antud andmete põhjal ei ole piisavalt tõendeid selle kohta, et andmed ei oleks normaaljaotusega.
Täiendavad kaalutlused
- Praktiline olulisus. Kuigi test näitab, et andmed ei pruugi olla täpselt normaaljaotusega, võib see kõrvalekalle olla piisavalt väike, et mitte mõjutada oluliselt järgnevaid statistilisi analüüse.
- Visuaalne kontroll. Lisaks testile on alati kasulik andmeid visuaalselt kontrollida näiteks histogrammi või Q-Q graafiku abil. See aitab paremini mõista andmete jaotust ja võimalikke kõrvalekaldeid.
Kokkuvõtteks. Shapiro-Wilki testi tulemus näitab, et andmed on tõenäoliselt normaaljaotusega, kuid alati on hea mõelda ka andmete praktilisele olulisusele ja neid visuaalselt kontrollida.
7.4 Lineaarne regressioon mitme tunnusega
Koostame mitmese lineaarse regressiooni, kus võraalguse kõrgus ennustatakse diameetri ja kõrgus alusel (HV = D + H).
Koostame mudeli, mille valem on HV~D+H.
Call:
lm(formula = HV ~ D + H, data = andmed)
Residuals:
Min 1Q Median 3Q Max
-1,2054 -0,4429 0,0429 0,4105 1,4123
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1,1089 0,6170 1,80 0,082
D -0,3601 0,0638 -5,65 3,4e-06
H 0,7795 0,0966 8,07 4,1e-09
Residual standard error: 0,627 on 31 degrees of freedom
Multiple R-squared: 0,689, Adjusted R-squared: 0,669
F-statistic: 34,3 on 2 and 31 DF, p-value: 1,37e-08Analysis of Variance Table
Response: HV
Df Sum Sq Mean Sq F value Pr(>F)
D 1 1,39 1,39 3,55 0,069
H 1 25,60 25,60 65,15 4,1e-09
Residuals 31 12,18 0,39 Mudeli ANOVA test näitab, et diameetri mõju ei pruugi olla oluline.
# Koostame täiendava mudeli, mis sõltub ainult kõrgusest
lm_4 <- lm(HV~H, andmed)
# Võrdleme kahte mudelit omavahel
aov_2 <- anova(lm_4, lm_3)Tulemusest on näha, et täiendavalt diameetrit sisaldav mudel on oluliselt (p-väärtus 3,37587^{-6}) täpsem, kui ainult kõrgusest sõltuv mudel.
Kasutame funktsiooni termplot(), et hinnata regressioonimudeli üksikute terminite mõju visualselt. See aitab mõista, kuidas iga argumenttunnus mõjutab funktsioontunnust, kui kõik teised tunnused hoitakse konstantsena.
- Regressioonimudel. Esiteks pead looma regressioonimudeli (lineaarne, üldistatud lineaarne või mõni muu), kasutades näiteks funktsioone nagu
lmvõiglm. termplot()funktsioon. Seejärel kasutad funktsioonitermplot, andes sellele mudeli ja määrates, milliseid termineid (tunnuseid) soovid visualiseerida.- Graafik.
termplotloob graafiku, kus x-teljel on konkreetse tunnuse väärtused ja y-teljel on selle tunnuse mõju vastussuurusele. Graafik näitab, kuidas vastussuurus muutub, kui tunnuse väärtus muutub, hoides samal ajal kõik teised tunnused konstantsena.
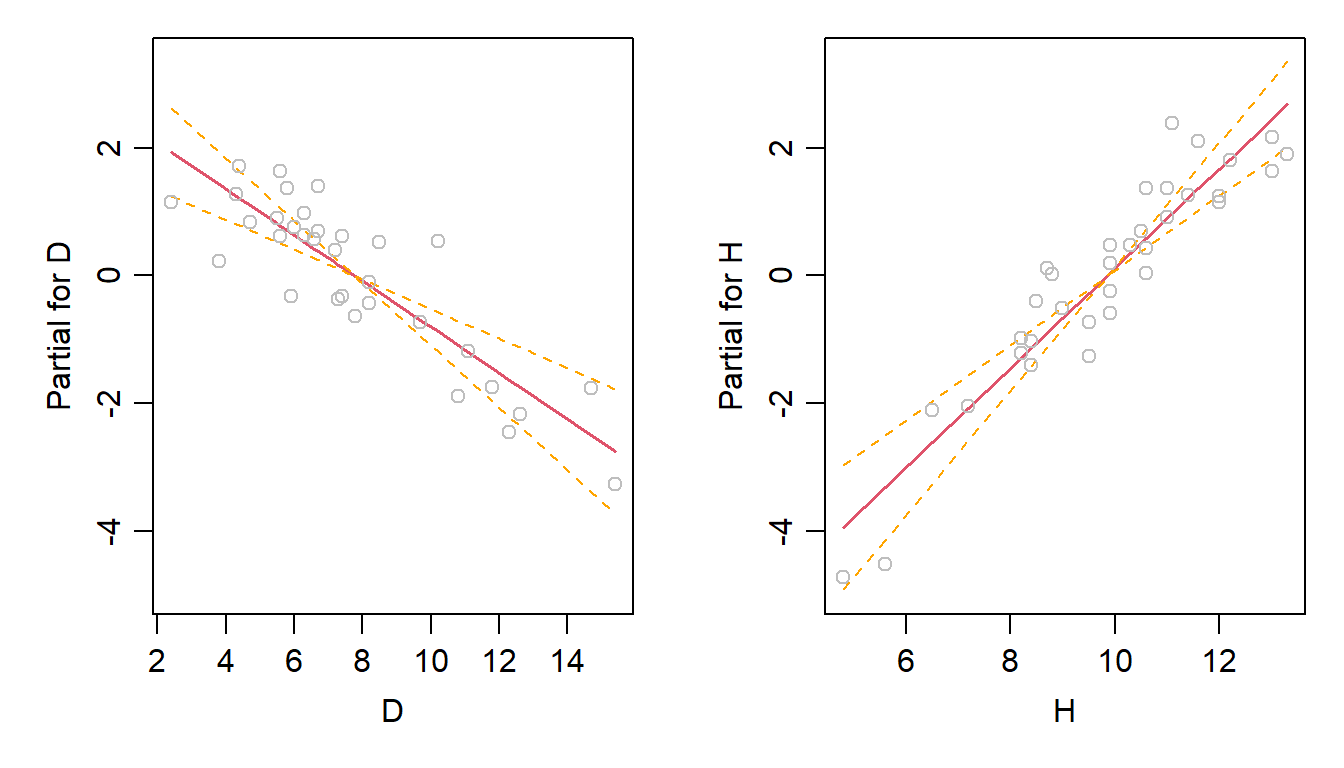
Joonis 7.4. Argumenttunnuste mõju funktsioontunnusele.
Olulised parameetrid
model. Regressioonimudel, mille jaoks termplot luuakse.terms. Vektor, mis määrab, milliseid termineid (tunnuseid) soovitakse visualiseerida.partial.resid. Loogiline väärtus, mis määrab, kas graafikule lisatakse osalised jäägid.se. Loogiline väärtus, mis määrab, kas graafikule lisatakse standardvead.
Vaatame tunnuste omavahelist korrelatsiooni ning sellest näeme, et D ja H vahel on tugev korrelatsioon. See mõjutab ka mudeli parameetreid.
D H HV
D 1,00000 0,82967 0,18860
H 0,82967 1,00000 0,60777
HV 0,18860 0,60777 1,00000