Peatükk 5 Jaotusfunktsioonid

5.1 Hüpotees

Hüpotees on statistikas ja teadusuuringutes oluline mõiste, mis kujutab endast oletust või väidet üldkogumi kohta, mida soovitakse testida. Hüpoteesid on aluseks statistilisele analüüsile, võimaldades teha järeldusi valimi põhjal üldkogumi kohta. Hüpoteeside kontrollimise eesmärk on otsustada, kas andmed toetavad teatud väidet või mitte.

Hüpoteeside liigid

Nullhüpotees (\(H_0\)). Nullhüpotees on väide, mille kohaselt oletatav seos või erinevus puudub, uuritav faktor ei mõjuta tunnuse jaotust või üldkogumi parameeter on võrdne teatud väärtusega. See on hüpotees, mida soovitakse ümber lükata või mille kehtivust testitakse. Nullhüpotees on seisukoht, mis kehtib vaikimisi, kuni on olemas piisavalt tõendeid selle ümberlükkamiseks. Näiteks võidakse püstitada nullhüpotees, et kahe grupi keskmised väärtused on võrdsed või et mingi muutuja jaotust ei mõjuta teine muutuja. Nullhüpoteesi püstitamine peab võimaldama selle ümberlükkamist.

Sisukas hüpotees (\(H_1\)). Sisukas hüpotees, mida nimetatakse ka alternatiivseks hüpoteesiks, on väide, mis on nullhüpoteesile vastand. See väljendab uurija ootust või arvamust, et mingi seos või erinevus on olemas või et uuritav faktor mõjutab tunnuse jaotust. Sisukas hüpotees on see, mida uurija soovib tõestada, seega on uurimise eesmärk leida piisavalt tõendeid, mis toetaksid sisuka hüpoteesi vastuvõtmist ja nullhüpoteesi ümberlükkamist. Näiteks, et kahe grupi keskmised väärtused erinevad või et mingi muutuja jaotus on mõjutatud teisest muutujast.

Hüpoteeside püstitamine. Hüpoteese püstitatakse üldkogumi, mitte valimi kohta. Hüpoteeside kontrollimise loogika algab eeldusest, et nullhüpotees kehtib ning uuritakse, kui tõenäoline on antud andmete saamine nullhüpoteesi kehtimise korral. Hüpoteese on alati kaks, sest need peavad teineteist välistama. Üldjuhul on nii, et ühte hüpoteesi ümber lükates, võetakse vastu teine hüpotees.

Hüpoteeside testimine. Hüpoteeside testimisel arvutatakse valimi andmete põhjal teststatistik. Teststatistiku väärtust võrreldakse teoreetilise jaotusega, mis on teada nullhüpoteesi kehtivuse korral. Kui valimi põhjal arvutatud teststatistiku väärtus on ebatõenäoline, loetakse nullhüpotees ümber lükatuks ja sisukas hüpotees tõestatuks. Oluline on mõista, et hüpoteese ei saa tõestada, vaid saab leida tõendeid nende toetuseks või vastuoluks. Kui andmed ei anna piisavalt tõendeid sisuka hüpoteesi kasuks, jäädakse nullhüpoteesi juurde. See ei tähenda, et nullhüpotees on tõestatud, vaid seda, et ei leitud piisavalt tõendeid selle ümberlükkamiseks.

Vead hüpoteeside kontrollimisel. Hüpoteeside kontrollimisel on võimalik teha kaht liiki vigu:

I liiki viga (\(\alpha\)). I liiki viga tekib siis, kui otsustatakse sisukas hüpotees vastu võtta, kuigi tegelikult on õige nullhüpotees. See on vale positiivne järeldus, mis tähendab, et leitakse seos või erinevus, mida tegelikult ei ole. I liiki vea tegemise tõenäosust nimetatakse olulisuse nivooks ja tähistatakse sümboliga \(\alpha\). Üldiselt on I liiki vea tõenäosus seatud tasemele 0,05, mis tähendab, et on 5% tõenäosus teha viga, kui nullhüpotees on õige. I liiki viga on enamasti raskemate tagajärgedega. I liiki vea tõenäosuse vähendamiseks tuleb vähendada olulisuse nivood.

II liiki viga (\(\beta\)). II liiki viga tekib siis, kui jäädakse nullhüpoteesi juurde, kuigi tegelikult on õige sisukas hüpotees. See on vale negatiivne järeldus, mis tähendab, et jäetakse leidmata seos või erinevus, mis tegelikult eksisteerib. II liiki viga on kergem viga, sest see tavaliselt tähendab, et soovitud tulemuste saamiseks on vaja rohkem andmeid koguda. Olulisuse nivoo vähendamine suurendab II liiki vea tõenäosust.

Hüpoteeside liigid vastavalt suunale:

Kahepoolne hüpotees. Kahepoolse hüpoteesi puhul testitakse, kas üldkogumi parameeter erineb teatud väärtusest, ilma et oleks määratud erinevuse suund. Näiteks, kas kahe grupi keskmised väärtused on erinevad (\(H_1: \mu_1 \neq \mu_2\)). Kahepoolse hüpoteesi korral on kriitiline piirkond mõlemal pool jaotuse keskmist.

Ühepoolne hüpotees. Ühepoolse hüpoteesi puhul testitakse, kas üldkogumi parameeter on suurem või väiksem teatud väärtusest. Ühepoolse hüpoteesi korral on kriitiline piirkond ühel pool jaotuse keskmist. Näiteks, kas ühe grupi keskmine on suurem kui teise grupi keskmine (\(H_1: \mu_1 > \mu_2\)) või vastupidi (\(H_1: \mu_1 < \mu_2\)).

Järgnevalt nimekiri täiendavatest statistika mõistetest, mida on oluline tunda hüpoteesi testimisel:

Testimise protsess:

Valim. Populatsioonist võetud vaatluste kogum, mida kasutatakse hüpoteesi testimiseks.
Valimstatistik. Valimist arvutatud väärtus, mis iseloomustab valimit (nt keskmine, standardhälve).
Teststatistik. Arvutatud väärtus, mis võrdleb valimi statistikat nullhüpoteesis oletatud väärtusega.
P-väärtus. Tõenäosus saada valimi statistika, mis on sama ekstreemne või ekstreemsem kui tegelikult saadud statistika, eeldades, et nullhüpotees on tõene.
Olulisuse nivoo (\(\alpha\)). Ettenähtud tõenäosuse piir, mille alusel otsustatakse nullhüpotees ümber lükata. Tavaliselt on see 0,05 või 0,01.
Järeldus. Otsus, kas lükata nullhüpotees ümber või mitte, tuginedes p-väärtuse ja olulisuse nivoo võrdlemisele.

Muud olulised mõisted:

Ühepoolne test. Hüpoteesi test, kus alternatiivne hüpotees määratleb suuna (nt keskmine on suurem kui).
Kahepoolne test. Hüpoteesi test, kus alternatiivne hüpotees ei määra suunda (nt keskmine on erinev).
Usaldusnivoo. Usaldusvahemikuga seotud kindluse tase, mis näitab usaldusvahemiku katvustõenäosust.
Usaldusvahemik. Väärtuste vahemik, mis teatud usaldusnivooga sisaldab populatsiooni parameetri tegelikku väärtust.
Vabadusastmete arv. Vaatlusandmete arv, mis on vabad varieeruma pärast statistiliste parameetrite hindamist.
Jaotus. Statistiline funktsioon, mis kirjeldab juhusliku muutuja võimalike väärtuste ja nende esinemise tõenäosusi (nt normaaljaotus, t-jaotus).

5.2 Jaotusfunktsioon

Jaotusfunktsioon on matemaatilise statistika mõiste, mis kirjeldab juhusliku suuruse väärtuste jaotust tõenäosuste kaudu. See seob iga juhusliku muutuja võimaliku väärtusega tõenäosuse, et muutuja väärtus on sellest väärtusest väiksem või sellega võrdne. Jaotusfunktsiooni tähistatakse tavaliselt \(F(x)\) või \(F_X(a)\), kus \(x\) või \(a\) tähistab reaalarvu, mille kohta tõenäosust arvutatakse. Seega,

\[F(x) = P(X \leq x),\]

kus \(X\) on juhuslik suurus ja \(P(X \leq x)\) on tõenäosus, et \(X\) võtab väärtuse, mis on väiksem või võrdne \(x\)-ga.

Jaotusfunktsiooni olemus

Kumulatiivne tõenäosus. Jaotusfunktsioon esitab kumulatiivset tõenäosust, st see näitab, kui suure tõenäosusega on juhusliku suuruse väärtus mingist antud väärtusest väiksem või sellega võrdne.

Diskreetse juhusliku suuruse jaotusfunktsioon. Diskreetse muutuja puhul, mille väärtused on eraldiseisvad (nt täisarvud), on jaotusfunktsioon treppfunktsioon, mis kasvab hüppeliselt iga võimaliku väärtuse juures. Jaotusfunktsiooni väärtus on sel juhul iga konkreetse väärtuse tõenäosuste summa. Kui \(p_i\) on tõenäosus, et \(X = x_i\), siis diskreetse muutuja jaotusfunktsiooni võib kirjutada kui

\[F(a) = \sum_{x_i \leq a} p_i.\]

Pideva juhusliku suuruse jaotusfunktsioon. Pideva muutuja puhul, mille väärtused võivad olla mistahes arvud teatud vahemikus (nt pikkus, kaal), on jaotusfunktsioon pidev. Pideva muutuja puhul on iga üksiku väärtuse tõenäosus null, seega kasutatakse tihedusfunktsiooni, mis kirjeldab muutuja väärtuste jaotumist. Jaotusfunktsioon on sel juhul tihedusfunktsiooni \(f(x)\) integraal:

\[F(x) = \int_{-\infty}^{x} f(t) dt.\]

Graafiliselt vastab integraalile graafikualuse ala pindala integreeritavas vahemikus, mis tähendab, et sündmuse tõenäosus kuuluda etteantud väärtusvahemikku on võrdne väärtusvahemikku jääva tihedusfunktsiooni aluse pindalaga.

Jaotusfunktsiooni omadused. Jaotusfunktsioon on mittekahanev, mis tähendab, et see ei saa kahaneda, kui argument suureneb. Jaotusfunktsiooni piirväärtused on 0 ja 1, st \(\lim_{x \to -\infty} F(x) = 0\) ja \(\lim_{x \to \infty} F(x) = 1\), mis tähendab, et tõenäosus on vahemikus 0 ja 1. Samuti on jaotusfunktsioon paremalt pidev.

Kasutusalad. Jaotusfunktsiooni abil saab leida tõenäosusi, et juhuslik suurus \(X\) on väiksem või võrdne mingi arvuga \(a\) (\(P(X \leq a)\)), suurem mingist arvust \(b\) (\(P(X > b) = 1 - P(X \leq b)\)), või asub mingis vahemikus \(a\) kuni \(b\) (\(P(a < X \leq b) = F(b) - F(a)\)). Jaotusfunktsioon on oluline tööriist mitmesugustes statistilistes analüüsides ja modelleerimises.

Näide

Kui meil on juhuslik suurus \(X\), mis näitab mündiviske tulemust (0 = “kiri” ja 1 = “kull”), siis jaotusfunktsioon oleks järgmine:

\(F(x) = 0\), kui \(x < 0\)
\(F(x) = 0,5\), kui \(0 \leq x < 1\)
\(F(x) = 1\), kui \(x \geq 1\)

See näide illustreerib diskreetse jaotusfunktsiooni, kus tõenäosus hüppab 0-lt 0,5-le ja sealt 1-le.

Seos tihedusfunktsiooniga

Pideva juhusliku suuruse puhul on tihedusfunktsioon \(f(x)\) jaotusfunktsiooni tuletis, ja jaotusfunktsioon on tihedusfunktsiooni integraal. Tihedusfunktsioon kirjeldab tõenäosustihedust juhusliku suuruse väärtuse ümber, ja jaotusfunktsioon kirjeldab kumulatiivset tõenäosust kuni teatud väärtuseni. Seega:

\[f(x) = \frac{dF(x)}{dx}\]

Jaotusfunktsiooni abil on võimalik arvutada tõenäosusi erinevate sündmuste toimumiseks. See on aluseks paljudele statistilistele meetoditele ja mudelitele, mis aitavad mõista ja prognoosida juhuslike suuruste käitumist.

5.3 Normaaljaotus

Normaaljaotus, tuntud ka kui Gaussi jaotus, on pidev sümmeetriline jaotus, mida iseloomustab kellakujuline tihedusfunktsiooni graafik. See on statistikas üks olulisemaid jaotusi, kuna paljud juhuslikud suurused on ligikaudu normaaljaotusega või on teisendatavad normaaljaotusele alluvaks.

Põhiomadused

Sümmeetria. Normaaljaotus on sümmeetriline keskväärtuse (\(\mu\)) suhtes. Keskväärtus, mediaan ja mood langevad kokku.

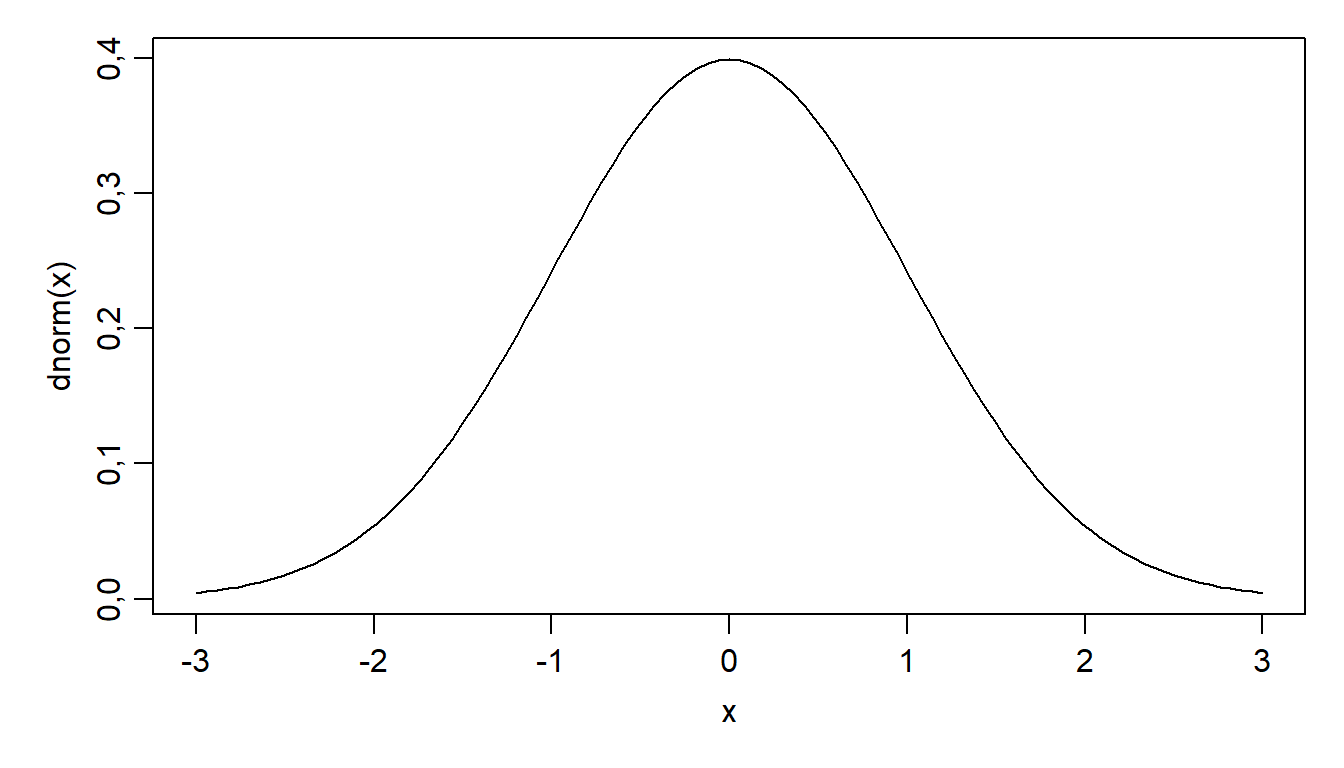
Joonis 5.1. Normaaljaotuse tihedusfunktsioon.

Tihedusfunktsioon. Normaaljaotuse tihedusfunktsioon on defineeritud järgmiselt:

\[f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]

kus:

\(\mu\) on jaotuse keskväärtus (määrab jaotuskõvera asukoha).
\(\sigma\) on standardhälve (määrab jaotuskõvera laiuse - suurem \(\sigma\) tähendab laiemat ja madalamat kõverat).

Tõenäosused ja standardhälve.

\(P(\mu - \sigma \le X \le \mu + \sigma) \approx 0,683\) (68,3% väärtustest jääb \(\pm 1\sigma\) vahemikku).
\(P(\mu - 2\sigma \le X \le \mu + 2\sigma) \approx 0,954\) (95,4% väärtustest jääb \(\pm 2\sigma\) vahemikku).
\(P(\mu - 3\sigma \le X \le \mu + 3\sigma) \approx 0,997\) (99,7% väärtustest jääb \(\pm 3\sigma\) vahemikku).

Standardiseeritud normaaljaotus (Z-jaotus). Normaaljaotusega juhuslik suurus \(X\) saab teisendada standardiseeritud normaaljaotusele \(Z\) järgmise valemiga:

\[z = \frac{x - \mu}{\sigma}\]

Standardiseeritud normaaljaotuse puhul \(\mu = 0\) ja \(\sigma = 1\), tähistatakse \(N(0,1)\).

Jaotusfunktsioon. Kumulatiivne jaotusfunktsioon \(F(x)\) näitab tõenäosust \(P(X \le x)\) ja on tihedusfunktsiooni integraal. Normaaljaotuse jaotusfunktsioon on S-kujuline.

Kasutusalad

Statistilised järeldused. Normaaljaotus on aluseks paljudele statistilistele meetoditele (nt t-testid, ANOVA, regressioonanalüüs), mis sageli eeldavad andmete normaaljaotust. Suurte valimite puhul (n > 30) on võimalik teatud piirini eirata andmete kõrvalekaldumist normaaljaotusest.

Protsesside modelleerimine. Paljud looduslikud ja majanduslikud nähtused on ligikaudu normaaljaotusega, olles mõjutatud mitmetest sõltumatutest juhuslikest teguritest.

Eelised ja piirangud.

Eelised:

Lihtne matemaatiline kirjeldus kahe parameetriga (\(\mu\) ja \(\sigma\)).
Laialdane kasutus ja põhjalikud teoreetilised alused.
Aluseks paljudele statistilistele testidele.
Tsentraalne piirteoreem tagab rakendatavuse valimite keskmiste analüüsil.

Piirangud:

Ei sobi kõikide andmetüüpidega, eriti tugeva asümmeetria või erindite korral.
Reaalsed andmed harva täielikult vastavad normaaljaotusele.
Ebasobivate andmete korral võib anda eksitavaid tulemusi.

5.4 T-jaotus

T-jaotus, tuntud ka kui Studenti t-jaotus, on pidev tõenäosusjaotus, mis meenutab normaaljaotust, olles lamedam ja laiema sabaga. See on eriti kasulik statistikas väikeste valimite puhul (tavaliselt alla 30) ja kui üldkogumi standardhälve pole teada. T-jaotust rakendatakse peamiselt hüpoteeside testimisel, usaldusvahemike leidmisel ja valimi keskmise võrdlemisel üldkogumi keskväärtusega. T-jaotuse kuju sõltub vabadusastmete arvust (df - degrees of freedom), mis on seotud valimi suurusega. Mida suurem on vabadusastmete arv, seda enam sarnaneb t-jaotus normaaljaotusega.

T-jaotuse omadused ja tunnused

Sümmeetria. T-jaotus on sümmeetriline nulli ümber, sarnaselt standardsele normaaljaotusele. See tähendab, et jaotuse mõlemad pooled on keskmisest võrdsel kaugusel.

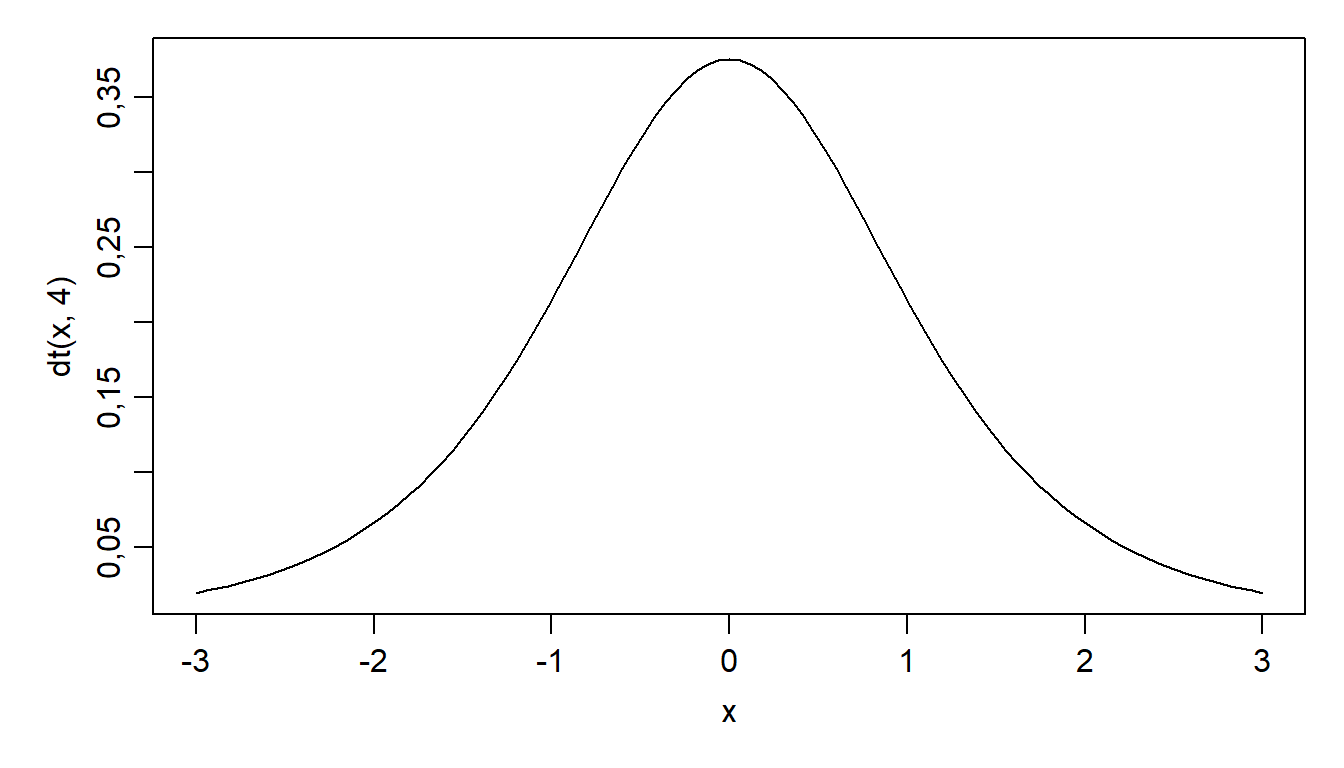
Joonis 5.2. T-jaotuse tihedusfunktsioon

Tihedusfunktsioon. T-jaotuse tihedusfunktsioon on keerukam kui normaaljaotusel ja sõltub vabadusastmete arvust. Valem on järgmine:

\[f(t) = \frac{\Gamma\left(\frac{\nu + 1}{2}\right)}{\sqrt{\nu\pi}\Gamma\left(\frac{\nu}{2}\right)} \left(1 + \frac{t^2}{\nu}\right)^{-\frac{\nu + 1}{2}}\]

kus \(\nu\) on vabadusastmete arv ja \(\Gamma\) on gammafunktsioon.

Vabadusastmed (df). T-jaotuse kuju määrab vabadusastmete arv. See arvutatakse valimi suuruse (\(n\)) põhjal. Ühe valimi t-testi korral on \(df = n - 1\), sõltumatute valimite t-testi korral \(df = n_1 + n_2 - 2\). Mida suurem on vabadusastmete arv, seda enam sarnaneb t-jaotus standardsele normaaljaotusele.

Keskväärtus ja dispersioon. T-jaotuse keskväärtus on 0, kui vabadusastmed on suuremad kui 1 (\(\nu > 1\)). Dispersioon sõltub vabadusastmetest ja on suurem kui 1 (\(\frac{\nu}{\nu-2}\), kui \(\nu>2\)).

Kasutusala. T-jaotust kasutatakse peamiselt juhul, kui valimi suurus on väike (tavaliselt \(n < 30\)) ja üldkogumi standardhälve on teadmata. Sellisel juhul ei saa kasutada standardset normaaljaotust.

T-jaotuse rakendamine

Hüpoteeside testimine. T-jaotust kasutatakse hüpoteeside testimisel, kui võrreldakse valimi keskmist teatud väärtusega või kahe valimi keskmisi. Näiteks t-testi abil kontrollitakse, kas kahe grupi keskmised erinevad oluliselt. T-testid võivad olla ühepoolsed või kahepoolsed. Ühepoolset testi kasutatakse siis, kui on teada, mis suunas hüpotees peaks erinema. Kahepoolset testi rakendatakse, kui soovitakse kontrollida, kas erinevus üldse on olemas.

Usaldusvahemikud. T-jaotust rakendatakse usaldusvahemike leidmisel, kui hinnatakse, millises vahemikus paikneb üldkogumi keskväärtus antud valimi põhjal. Usaldusvahemik näitab, kui suur on tõenäosus, et tegelik keskmine väärtus jääb antud piiridesse.

Regressioonanalüüs. Regressioonanalüüsis rakendatakse t-jaotust regressioonimudeli parameetrite olulisuse testimiseks. Näiteks, et teha kindlaks, kas mingi muutuja mõjutab sõltuvat muutujat statistiliselt olulisel määral. Regressioonanalüüsi käigus hinnatakse mudeli parameetreid ja iga parameetri kohta arvutatakse t-statistik, mille abil otsustatakse, kas vastav muutuja on oluline mudeli seletusjõu seisukohalt.

Järelduste tegemine väikeste valimitega. T-jaotus on hädavajalik, kui valim on väike. Sellisel juhul ei saa kasutada normaaljaotust, mis eeldab suuremat valimit usaldusväärsete järelduste tegemiseks. T-jaotus võimaldab teha järeldusi ka väikeste valimite puhul, arvestades ebakindlust, mis kaasneb väikese valimi kasutamisega.

Võrdlusülesanded. T-test on statistiline meetod, mida kasutatakse kahe valimi keskmiste võrdlemiseks, eeldades, et andmed on normaalselt jaotunud või valimi suurus on piisavalt suur.

T-testide liigid

Ühe valimi t-test. Kasutatakse, kui võrreldakse valimi keskmist teadaoleva või hüpoteetilise keskväärtusega.

Sõltumatute valimite t-test. Kasutatakse, kui võrreldakse kahe sõltumatu valimi keskmisi. See test eeldab, et andmed on mõlemas valimis ligikaudu normaalselt jaotunud ja et dispersioonid on ligikaudu võrdsed (või tehakse korrektsioon ebavõrdsete dispersioonide korral).

Sõltuvate valimite t-test. Kasutatakse, kui võrreldakse kahe sõltuva valimi keskmisi, kus iga vaatlus ühes valimis on seotud vastava vaatlusega teises valimis (näiteks mõõtmised enne ja pärast sekkumist).

T-statistiku arvutamine

T-statistiku arvutamise valem sõltub kasutatavast t-testist, kuid üldine idee on leida valimi keskmise hälve hüpoteetilisest keskväärtusest või kahe valimi keskmise erinevus, jagatuna standardveaga. Ühe valimi t-testi puhul on valem järgmine:

\[t = \frac{\bar{x} - \mu}{s / \sqrt{n}}\]

kus \(\bar{x}\) on valimi keskmine, \(\mu\) on hüpoteetiline keskväärtus, \(s\) on valimi standardhälve ja \(n\) on valimi suurus.

Vead t-testi rakendamisel

I liiki viga (\(\alpha\)). I liiki viga tekib siis, kui lükatakse tagasi nullhüpotees, kuigi see on tegelikult õige. See tähendab, et leitakse statistiliselt oluline erinevus, mida tegelikult ei ole. T-testi tulemustes on selle vea tõenäosus P(T<=t), mis tähistab tõenäosust, et t-statistik on võrdne või suurem antud väärtusest.

II liiki viga (\(\beta\)). II liiki viga tekib siis, kui ei lükata tagasi nullhüpoteesi, kuigi see on tegelikult vale. See tähendab, et ei leita statistiliselt olulist erinevust, kuigi see tegelikult eksisteerib.

Olulisuse nivoo. Enne testi tegemist valitakse olulisuse nivoo (\(\alpha\)), mis määrab tõenäosuse teha I liiki viga. Tavaliselt kasutatakse olulisuse nivood 0,05, mis tähendab, et on 5% tõenäosus teha I liiki viga. Olulisuse nivoo valik sõltub ka sellest, milliseid tagajärgi toob kaasa vea tegemine.

5.5 F-jaotus

F-jaotus on pidev tõenäosusjaotus, mida kasutatakse peamiselt dispersioonanalüüsis (ANOVA) ja hüpoteeside testimisel, eriti kahe või enama valimi dispersioonide võrdlemisel. See jaotus on statistikas oluline, kuna võimaldab hinnata, kas erinevused valimite dispersioonides on statistiliselt olulised või juhuslikud. F-jaotus on alati positiivne, sest see põhineb dispersioonide jagatisel, mis on alati positiivne.

F-jaotuse omadused ja tunnused

Pidevus. F-jaotus on pidev jaotus, mis tähendab, et see hõlmab kõiki positiivseid reaalarve.

Asümmeetria. F-jaotus on parempoolse kaldega, asümmeetriline jaotus. Jaotuse tihedusfunktsioon ei ole sümmeetriline, jaotuse “saba” ulatub paremale poole.

Parameetrid. F-jaotust iseloomustavad kaks parameetrit: lugeja vabadusastmete arv (k) ja nimetaja vabadusastmete arv (h). Need vabadusastmed on seotud võrreldavate valimite suurustega.

Vabadusastmed. Vabadusastmed (degrees of freedom) tähistavad sõltumatute andmepunktide arvu, mida saab kasutada dispersiooni hindamiseks. Vabadusastmete arv mõjutab oluliselt F-jaotuse kuju. Tihedusfunktsioon. F-jaotuse tihedusfunktsioon on defineeritud järgmiselt:

\[f(x) = \frac{\Gamma\left(\frac{k + h}{2}\right)}{\Gamma\left(\frac{k}{2}\right) \Gamma\left(\frac{h}{2}\right)} \left(\frac{k}{h}\right)^{\frac{k}{2}} x^{\frac{k}{2} - 1} \left(1 + \frac{k}{h} x\right)^{-\frac{k + h}{2}}, \quad x > 0\] kus \(x\) on argument, \(\Gamma\) on gammafunktsioon, \(k\) on lugeja vabadusastmete arv ja \(h\) on nimetaja vabadusastmete arv. Valem näitab, kuidas F-jaotuse tihedus muutub argumendi \(x\) väärtuste korral.

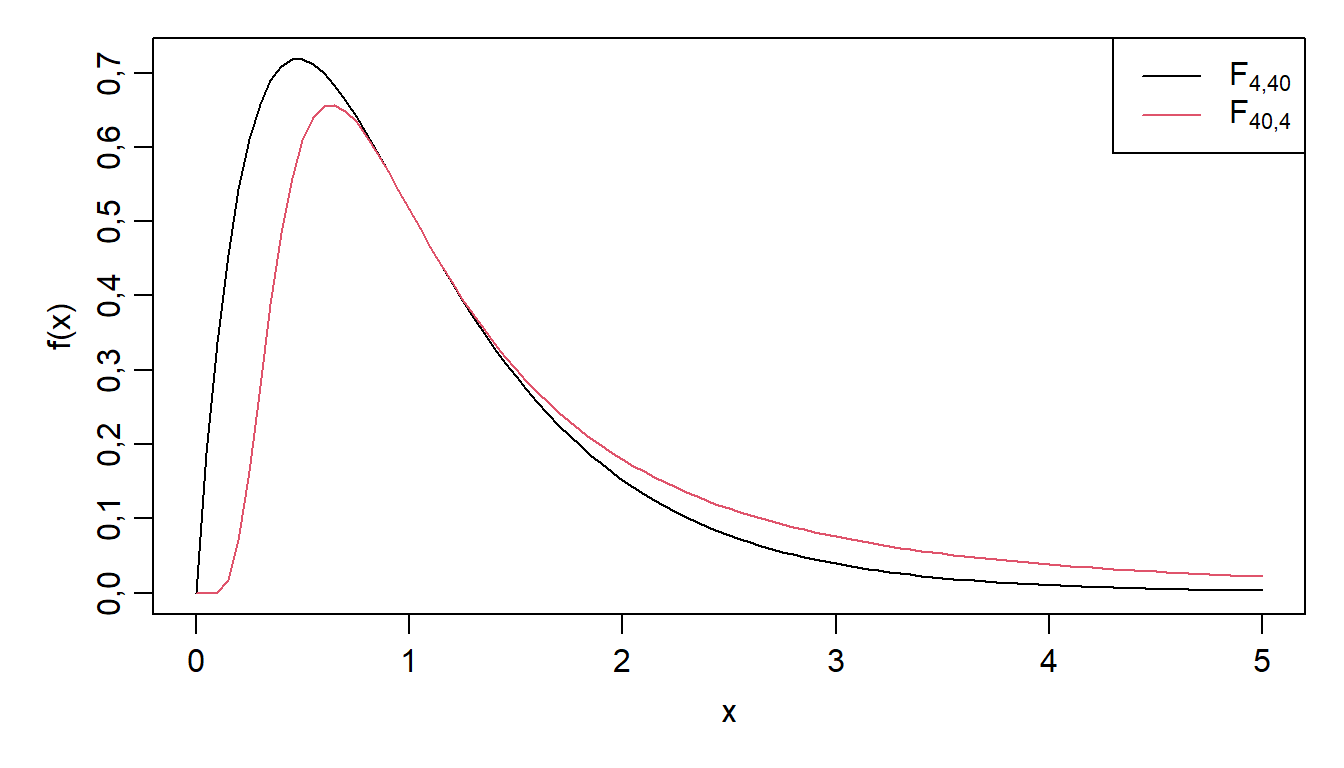
Joonis 5.3. T-jaotuse tihedusfunktsioon.

Väärtuste vahemik. F-jaotuse väärtused on alati positiivsed ja ulatuvad nullist lõpmatuseni.

Kuju sõltuvus vabadusastmetest. F-jaotuse kuju sõltub lugeja ja nimetaja vabadusastmetest. Suuremate vabadusastmete korral muutub jaotus sümmeetrilisemaks ja läheneb normaaljaotusele.

F-jaotuse rakendused.

Dispersioonanalüüs (ANOVA). F-jaotust kasutatakse peamiselt ANOVA-s, et testida, kas kahe või enama grupi keskmiste vahel on statistiliselt olulisi erinevusi. ANOVA-s arvutatakse F-statistik, mis on gruppidevahelise dispersiooni jagatis grupisisese dispersiooniga. Kui F-statistik on piisavalt suur, lükatakse tagasi nullhüpotees, mis väidab, et kõikide gruppide keskmised on võrdsed.

Hüpoteeside testimine. F-jaotust rakendatakse hüpoteeside testimisel, eriti dispersioonide võrdlemisel. Näiteks Levene’i test kasutab F-jaotust, et kontrollida, kas kahe või enama valimi dispersioonid on võrdsed. Seda tehakse sageli enne t-testi või ANOVA-t, veendumaks, et eeldus dispersioonide võrdsusest on täidetud.

Regressioonanalüüs. F-jaotust kasutatakse regressioonanalüüsis mudeli sobivuse hindamiseks. F-testi abil hinnatakse, kas regressioonimudel seletab olulisel määral sõltuva muutuja varieeruvust, võrreldes mudeliga, mis ei sisalda ühtegi seletavat muutujat.

Kahe dispersiooni võrdlemine. Kahe valimi dispersiooni võrdlemiseks kasutatakse F-testi, mis põhineb F-jaotusel. Teststatistiku arvutamiseks jagatakse suurem dispersioon väiksemaga. Seejärel võrreldakse saadud väärtust F-jaotuse kriitilise väärtusega, et teha kindlaks statistiline olulisus.

Mudelite võrdlemine. F-jaotust saab rakendada ka erinevate statistiliste mudelite võrdlemiseks, et selgitada välja, milline mudel sobib andmetega paremini. Näiteks mitme lineaarse regressiooni mudeli puhul saab F-testi abil võrrelda mudelite seletusjõudu ja parameetrite olulisust.

F-statistiku arvutamine

F-statistiku arvutamise täpne valem sõltub konkreetsest testist või analüüsist, kuid üldpõhimõte on dispersioonide võrdlemine.

ANOVA-s defineeritakse F-statistik järgmiselt:

\[F = \frac{MST}{MSE}\]

kus \(MST\) on rühmadevaheline keskmine ruut (mean square between groups) ehk seletatud hajumine ja \(MSE\) on rühmasisene keskmine ruut (mean square within groups) ehk seletamata hajumine.

Kahe dispersiooni võrdlemisel arvutatakse F-statistik järgmiselt:

\[F = \frac{s_1^2}{s_2^2}\] kus \(s_1^2\) on suurem dispersioon ja \(s_2^2\) on väiksem dispersioon.

F-jaotuse seos teiste jaotustega

\(\chi^2\)-jaotus. F-jaotus on tihedalt seotud \(\chi^2\)-jaotusega. Kui kaks sõltumatut juhuslikku suurust \(X_k\) ja \(X_h\) alluvad \(\chi^2\)-jaotusele vabadusastmetega \(k\) ja \(h\), siis avaldis \(\frac{X_k/k}{X_h/h}\) allub F-jaotusele vabadusastmetega \(k\) ja \(h\).

T-jaotus. F-jaotust saab kasutada t-jaotuse tulemuste tuletamiseks. Kui \(t\) allub t-jaotusele vabadusastmega \(v\), siis \(t^2\) allub F-jaotusele vabadusastmetega 1 ja \(v\). Seega saab F-jaotust kasutada näiteks kahe valimi t-testi tulemuste kontrollimiseks ja usaldusväärsuse hindamiseks.

Vead F-testi rakendamisel

I liiki viga (\(\alpha\)). I liiki viga tekib, kui lükatakse tagasi tõene nullhüpotees. See tähendab, et leitakse statistiliselt oluline erinevus, mida tegelikult ei eksisteeri.

II liiki viga (\(\beta\)). II liiki viga tekib, kui jäetakse tagasi lükkamata vale nullhüpotees. See tähendab, et ei leita statistiliselt olulist erinevust, mis tegelikult eksisteerib.

5.6 \(\chi^2\)-jaotus (hii-ruut-jaotus)

\(\chi^2\)-jaotus ehk hii-ruut-jaotus on pidev tõenäosusjaotus, mida kasutatakse statistikas laialdaselt erinevate hüpoteeside testimiseks, eriti kategooriliste andmete puhul või dispersioonide hindamisel. See jaotus on asümmeetriline ja omab olulist rolli mitmetes statistilistes testides.

\(\chi^2\)-jaotuse omadused ja tunnused

Pidevus. \(\chi^2\)-jaotus on pidev, mis tähendab, et see võib omandada mis tahes positiivseid väärtusi.

Asümmeetria. Jaotus on parempoolse kaldega, st jaotuse saba ulatub paremale ja tihedusfunktsioon ei ole sümmeetriline. Mida suurem on vabadusastmete arv, seda sümmeetrilisemaks jaotus muutub, lähenedes normaaljaotusele.

Parameetrid. \(\chi^2\)-jaotust iseloomustab üks parameeter: vabadusastmete arv (\(n\)). Vabadusastmed on seotud valimi suuruse ja analüüsis kasutatavate piirangutega.

Vabadusastmed. Vabadusastmed (degrees of freedom) tähistavad iseseisvate andmepunktide arvu, mis on kasutatavad dispersiooni hindamiseks. Vabadusastmete arv mõjutab oluliselt \(\chi^2\)-jaotuse kuju ja positsiooni.

Tihedusfunktsioon. \(\chi^2\)-jaotuse tihedusfunktsioon on määratud valemiga, kus parameetriks on vabadusastmete arv. Konkreetne valem on keeruline, aga oluline on teada, et see kirjeldab, kuidas \(\chi^2\)-jaotuse tihedus muutub sõltuvalt väärtusest ja vabadusastmetest.

Väärtuste vahemik. \(\chi^2\)-jaotuse väärtused on alati positiivsed ja ulatuvad nullist lõpmatuseni, kuna \(\chi^2\)-statistikud arvutatakse ruutude summana.

Seos normaaljaotusega. Kui sõltumatud juhuslikud suurused \(X_1, X_2, ..., X_n\) alluvad standardsele normaaljaotusele \(N(0, 1)\), siis nende ruutude summa, \(Y_n = \sum_{i=1}^n X_i^2\), allub \(\chi^2\)-jaotusele vabadusastmete arvuga \(n\). See seos on oluline, kuna see võimaldab seostada \(\chi^2\)-jaotust normaaljaotusega.

Keskväärtus ja dispersioon. \(\chi^2\)-jaotuse keskväärtus võrdub vabadusastmete arvuga (\(n\)) ja dispersioon on \(2n\).

\(\chi^2\)-jaotuse kasutamine

Hüpoteeside testimine. \(\chi^2\)-jaotust kasutatakse laialdaselt erinevate hüpoteeside testimiseks, eriti kategooriliste andmete puhul. See hõlmab järgmisi olukordi:

Sobivuse test. \(\chi^2\)-sobivuse test (goodness-of-fit test) hindab, kas empiiriliste andmete jaotus vastab teoreetilisele jaotusele. Näiteks, kas mündiviske tulemused vastavad ootusele, et mõlemad pooled on võrdselt tõenäolised.

Sõltumatuse test. \(\chi^2\)-sõltumatuse test (test of independence) uurib, kas kaks kategoorilist muutujat on omavahel sõltuvad. Näiteks, kas haridustase ja sotsiaalmajanduslik staatus on omavahel seotud.

Homogeensuse test. \(\chi^2\)-homogeensuse test uurib, kas mitu valimit on pärit samast populatsioonist. Näiteks, kas erinevates piirkondades esineb samasugune osakaal erinevaid haridustasemeid.

Dispersiooni hindamine. \(\chi^2\)-jaotust kasutatakse ka valimi dispersiooni hindamisel, kui populatsioon on normaaljaotusega. Näiteks valimi standardhälbe usalduspiiride leidmisel.

Vastavusanalüüs. \(\chi^2\)-statistikut kasutatakse vastavusanalüüsis (correspondence analysis) kategooriliste muutujate vahelise seose hindamiseks ja visualiseerimiseks.

Teguranalüüs. \(\chi^2\)-testi kasutatakse ka teguranalüüsis, et hinnata mudeli sobivust andmetega.

Pideva juhusliku suuruse testimine. \(\chi^2\)-testi saab kasutada ka pidevate juhuslike suuruste korral, aga sel juhul tuleb variatsioonrida eelnevalt intervallida.

\(\chi^2\)-statistiku arvutamine

\(\chi^2\)-statistiku arvutamise valem sõltub testitavast hüpoteesist, aga üldine idee on võrrelda vaadeldud sagedusi oodatavate sagedustega. Üldiselt arvutatakse \(\chi^2\)-statistik järgmiselt:

\[\chi^2 = \sum_{i=1}^k \frac{(O_i - E_i)^2}{E_i}\]

kus \(O_i\) on vaadeldud sagedus \(i\)-ndas kategoorias ja \(E_i\) on oodatav sagedus \(i\)-ndas kategoorias. Oodatav sagedus arvutatakse nullhüpoteesi kehtivuse korral.

\(\chi^2\)-testi eeldused:

Sõltumatud vaatlused. Vaatlused peavad olema üksteisest sõltumatud.
Oodatavad sagedused. Oodatavad sagedused ei tohiks olla liiga väikesed (tavaliselt vähemalt 5 igas kategoorias). Liiga väikeste oodatavate sageduste korral võib test olla ebatäpne.
Kategoorilised andmed. \(\chi^2\)-test sobib peamiselt kategooriliste andmete analüüsiks. Pidevate andmete puhul tuleb need enne testi rakendamist kategooriatesse jaotada.

\(\chi^2\)-jaotuse seos teiste jaotustega

F-jaotus. \(\chi^2\)-jaotus on seotud F-jaotusega. Kui kaks sõltumatut \(\chi^2\)-jaotusega juhuslikku suurust jagatakse vastavate vabadusastmetega, siis nende jagatis allub F-jaotusele.
Normaaljaotus. Suure vabadusastmete arvu korral läheneb \(\chi^2\)-jaotus normaaljaotusele.

Vead \(\chi^2\)-testi rakendamisel

I liiki viga (\(\alpha\)). Esimest liiki viga tehakse siis, kui lükatakse tagasi nullhüpotees, kuigi see on tegelikult õige. See tähendab, et leitakse statistiliselt oluline erinevus, kuigi seda tegelikult ei ole.
II liiki viga (\(\beta\)). Teist liiki viga tehakse siis, kui ei lükata tagasi nullhüpoteesi, kuigi see on tegelikult vale. See tähendab, et ei leita statistiliselt olulist erinevust, kuigi see tegelikult eksisteerib.