Peatükk 9 Mitteparameetriline analüüs

9.1 Üldistatud aditiivne mudel

Üldistatud aditiivne mudel (GAM) on statistiline mudel, mis ühendab lineaarse mudeli omadused aditiivsete funktsioonide abil. Lihtsamalt öeldes on GAM mudel, mis modelleerib funktsioontunnust ühe või mitme argumenttunnuse summa abil, kus iga argumenttunnuse mõju funktsioontunnusele modelleeritakse splainfunktsiooni abil.

Splainfunktsioon on matemaatiline funktsioon, mida kasutatakse andmete interpoleerimiseks ja sujuvaks lähendamiseks. See on ühesuguse struktuuriga tükiti polünomiaalne funktsioon, mis on konstrueeritud nii, et see oleks sujuv ja pidev andmepunktide vahel. See tähendab, et splainfunktsioonil ei ole järske hüppeid ega nurki, mis teeb selle ideaalseks tööriistaks sujuvate kõverate ja pindade modelleerimiseks.

Selles näites kasutame R-i paketti mgcv GAM mudeli sobitamiseks. Eesmärk on modelleerida puu kõrguse ja diameetri vahelist seost, eeldades, et see seos ei pruugi olla lineaarne.

Kõigepealt laadime andmestiku, mis sisaldab puude kõrguse ja diameetri mõõtmiste andmeid.

# Laadime peatükis kasutatavad paketid
library(dplyr)
library(readxl)
library(mgcv)
# Andmete laadimine
andmed <- read_excel("data/naited.xlsx","prt_andmed") %>% filter(h > 0)

GAM mudeli lähendamiseks kasutame funktsiooni gam() paketist mgcv. Kasutame splainfunktsiooni diameetri muutuja jaoks, et modelleerida mittelineaarset seost.

# GAM mudeli sobitamine
mudel <- gam(h ~ s(d), data = andmed)

Selles koodis:

  • H ~ s(D) määrab mudeli valemi. H on funktsioontunnus ja s(D) määrab, et diameetri (D) mõju kõrgusele modelleeritakse sujuva funktsiooni s() abil.
  • data = andmed määrab andmestiku, mida kasutada.

3. Mudeli kokkuvõtte vaatamine.

Saame mudeli kohta detailse kokkuvõtte funktsiooni summary() abil:

# Mudeli kokkuvõte
summary(mudel)

Family: gaussian 
Link function: identity 

Formula:
h ~ s(d)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)   24,368      0,182     134   <2e-16

Approximate significance of smooth terms:
      edf Ref.df  F p-value
s(d) 3,68   4,61 24  <2e-16

R-sq.(adj) =  0,705   Deviance explained = 72,8%
GCV = 1,7242  Scale est. = 1,5525    n = 47

Kokkuvõte annab meile informatsiooni mudeli sobivuse kohta, sh:

  • Parametric coefficients. Kui mudelis on ka lineaarseid komponente, näidatakse siin nende koefitsiendid. Kuna mudelis ühtegi lineaarset tunnust ei ole kasutatud, siis on siin ainult vabaliige (Intercept).
  • Approximate significance of smooth terms. Siin näeme p-väärtuse hinnangut splainfunktsiooni olulisuse kohta. Madal p-väärtus (<0.05) viitab statistiliselt olulisele mittelineaarsele seosele diameetri ja kõrguse vahel.
  • R-sq.(adj). Korrigeeritud determinatsioonikordaja näitab, kui suure osa kõrguse varieeruvusest mudel seletab.
  • Deviance explained. Sarnane determinatsioonikordajale, näitab mudeli poolt seletatud hälbimuse osakaalu.

Kasutades funktsiooni coef(), näeme splainfunktsiooni polünoomi parameetrite väärtusi.

coef(mudel)
(Intercept)      s(d).1      s(d).2      s(d).3      s(d).4      s(d).5 
 24,3680851  -1,6514056  -0,8997401  -0,0019625   0,0345575  -0,0430375 
     s(d).6      s(d).7      s(d).8      s(d).9 
  0,1877321  -0,1323456  -0,8129444   3,4477405

Saame visualiseerida diameetri ja kõrguse vahelist seost funktsiooni plot() abil:

# Mudeli visualiseerimine
par(mar=c(4,4,1,1), mgp=c(2, 0.7, 0))
plot(mudel)
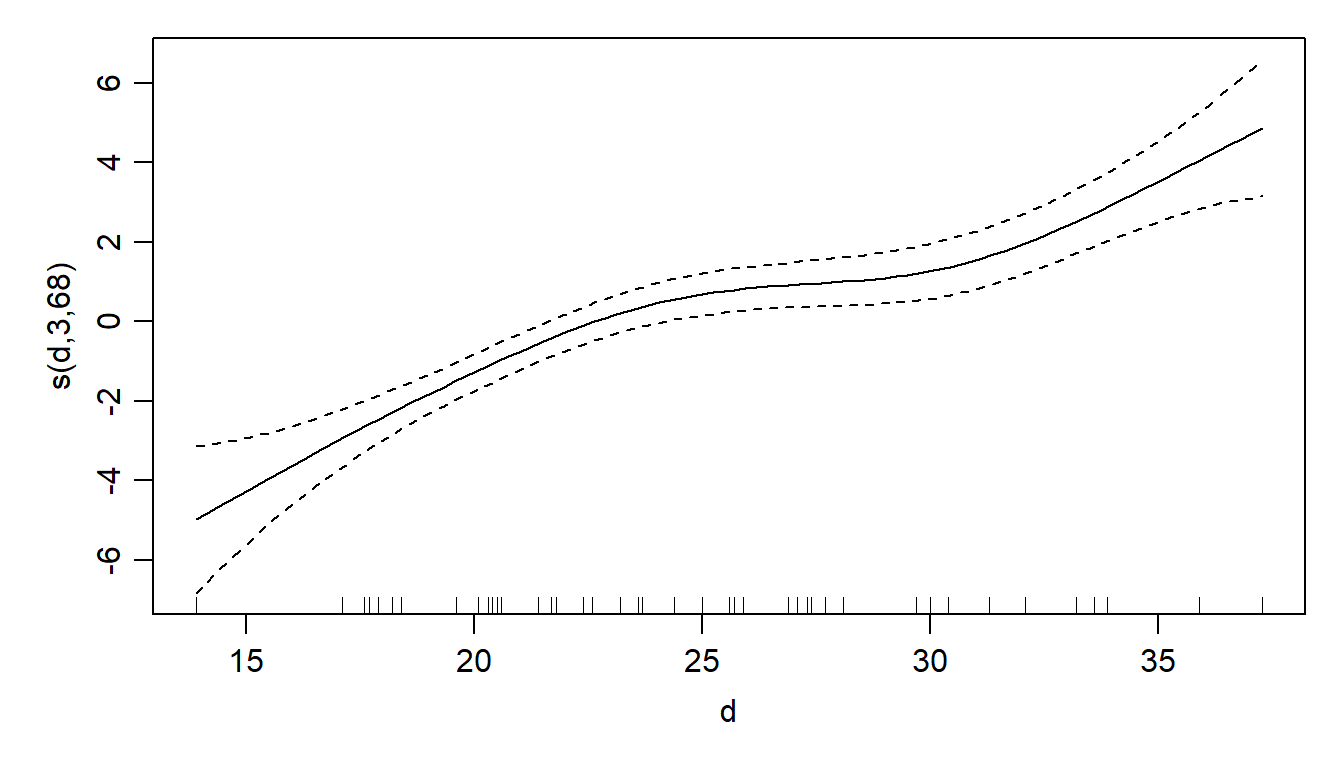
Kõrguse sõltuvus diameetrist

Joonis 9.1. Kõrguse sõltuvus diameetrist

See kuvab graafiku, mis näitab diameetri mõju puu kõrgusele. Pidevjoon näitab modelleeritud seost ja kriipsjooned näitavad usaldusvahemikku. See graafik aitab visuaalselt hinnata seose kuju ja mittelineaarsust.

Saame kasutada mudelit uute puude kõrguse ennustamiseks, andes ette diameetri väärtused funktsiooni predict() abil:

# Uute diameetrite väärtused
uued_andmed <- data.frame(d = c(12, 22, 32))

# Ennustuste tegemine
uued_andmed$h <- predict(mudel, newdata = uued_andmed)

# Ennustuste kuvamine
print(uued_andmed)
   d      h
1 12 18,134
2 22 24,092
3 32 26,298

9.2 Visualiseerimine paketiga ggplot2

Oletame, et meil on samad andmed puude kõrguse (h) ja diameetri (d) kohta nagu eelmistes näidetes, aga me tahame luua hajuvusdiagrammi ja lisada sellele sujuva joone otse ggplot2 abil, ilma et peaks eraldi gam() funktsiooni kasutama.

# Laadi pakett
library(ggplot2)

Kasutame ggplot() funktsiooni koos geom_point() ja geom_smooth() funktsioonidega:

ggplot(andmed, aes(x = d, y = h)) +
  geom_point() +  # Joonistab hajuvusdiagrammi
  geom_smooth(method = "gam", formula = y ~ s(x)) +  # Lisab sujuva joone GAM mudeli abil
  labs(x = "Diameeter (cm)", y = "Kõrgus (m)") +
  theme_bw()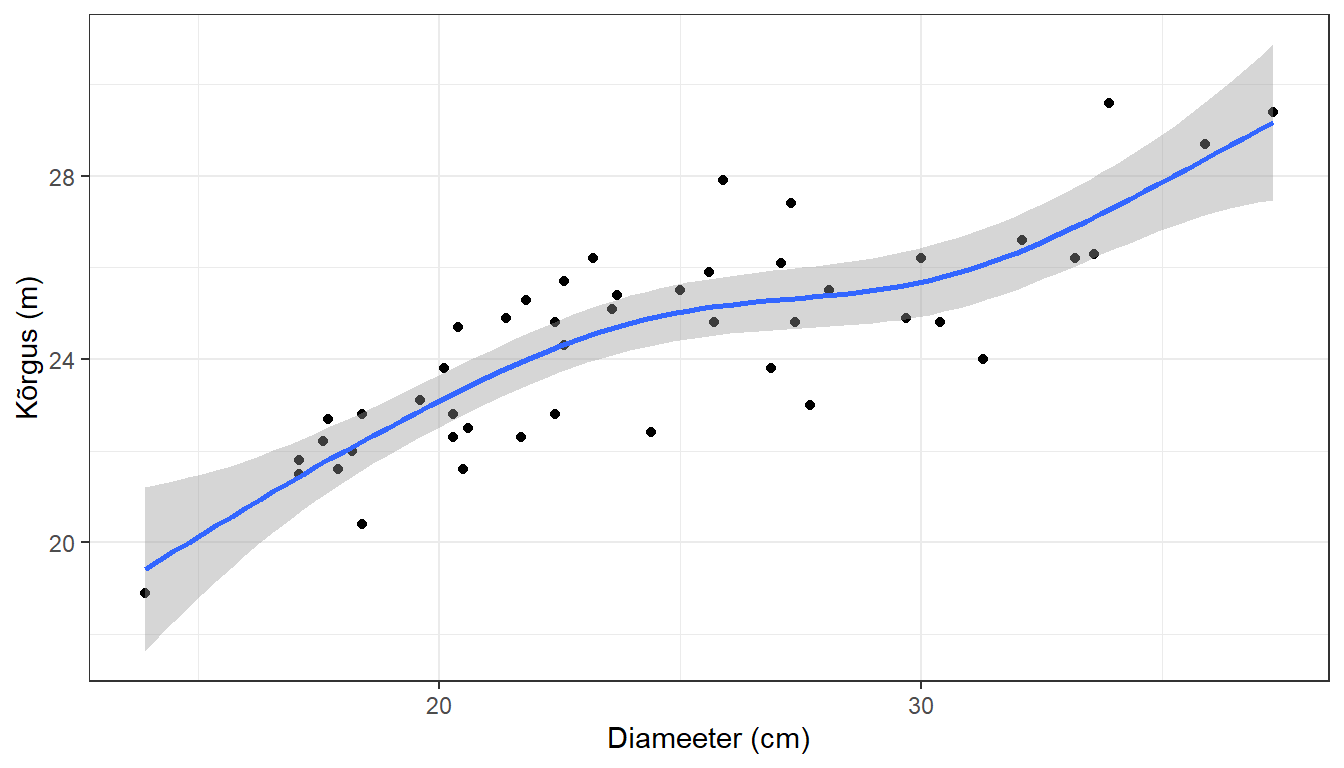
Kõrguse sõltuvus diameetrist

Joonis 9.2. Kõrguse sõltuvus diameetrist

Selgitus:

  • ggplot(puud, aes(x = d, y = h)): See rida loob ggplot objekti ja määrab andmestiku (andmed) ning x-telje (diameeter - D) ja y-telje (kõrgus - H) muutujad.
  • geom_point(): See funktsioon lisab graafikule punktid, luues hajuvusdiagrammi. Iga punkt esindab ühte puud.
  • geom_smooth(method = "gam", formula = y ~ s(x)): See funktsioon lisab graafikule sujuva joone.
    • method = "gam": Määrab, et sujuva joone sobitamiseks kasutatakse GAM mudelit.
    • formula = y ~ s(x): Määrab mudeli valemi. y ~ s(x) tähendab, et y (meie puhul kõrgus H) modelleeritakse x (meie puhul diameeter D) sujuva funktsiooni s() abil. See on sama valem, mida kasutasime eelmistes näidetes gam() funktsiooni sees.
  • labs(...): Määrab telgede sildid ja graafiku pealkirja.
  • theme_bw(): Muudab graafiku teema must-valgeks.

Sarnaselt eelmisele näitele saate ggplot2 abil graafikut vastavalt oma soovile kohandada. Näiteks:

ggplot(andmed, aes(x = d, y = h, color = pl)) +
  # Muudab punktide värvi, kuju ja suurust
  geom_point() +  
  # Eemaldab usaldusvahemiku ja muudab joone värvi
  geom_smooth(method = "gam", formula = y ~ s(x)) +  
  labs(x = "Diameeter (D)", y = "Kõrgus (H)") +
  theme_bw()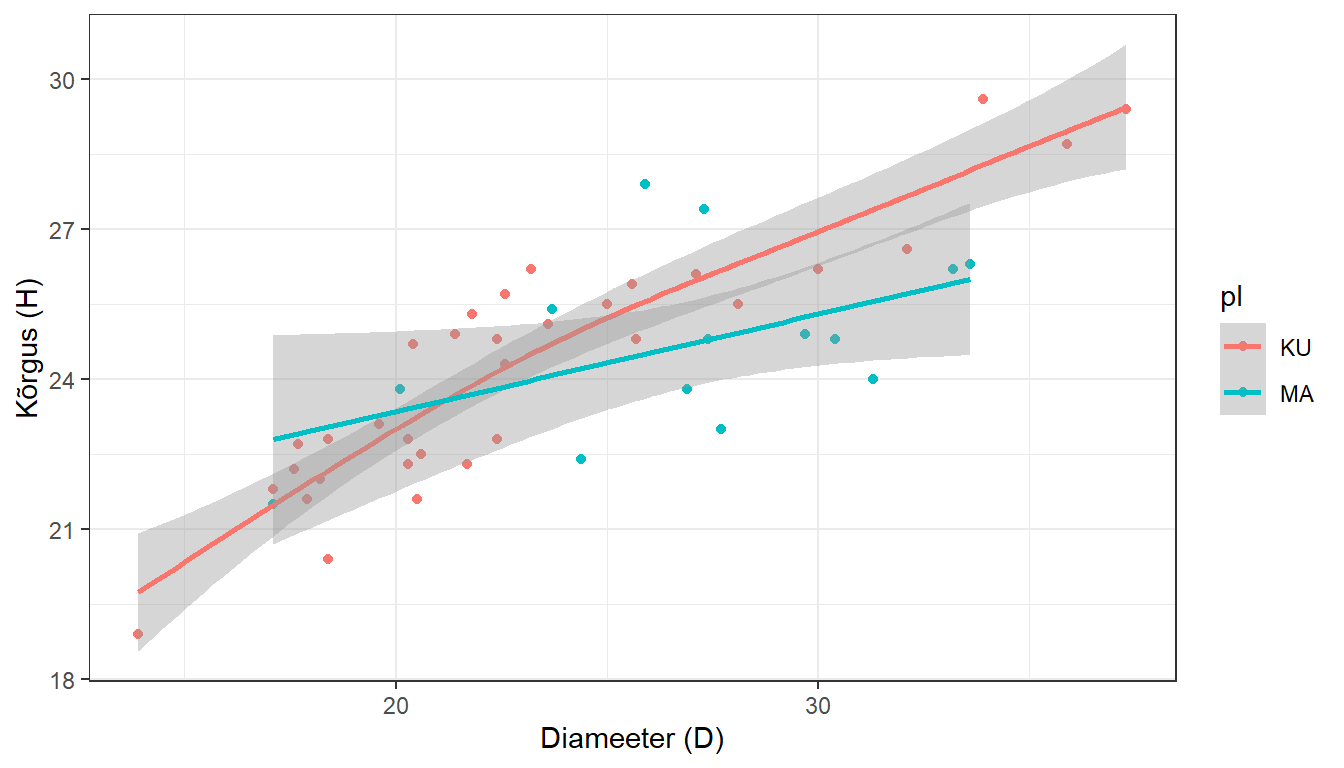
Kõrguse sõltuvus diameetrist

Joonis 9.3. Kõrguse sõltuvus diameetrist

Selles näites:

  • aes(x = D, y = H, color = PL) on lisatud, et värv sõltub puuliigist.

See näide demonstreerib, kuidas luua hajuvusdiagramm ja lisada sellele sujuv joon, mis on sobitatud GAM mudeli abil, kasutades ainult ggplot2 funktsioone. See on mugav viis kiiresti visualiseerida mittelineaarseid seoseid andmetes ilma eraldi GAM mudelit sobitamata. ggplot2 pakub laialdasi võimalusi graafikute kohandamiseks, võimaldades luua informatiivseid ja visuaalselt meeldivaid visualiseeringuid.